Flächeninhalt des Vierecks

Bei der Berechnung des Flächeninhalts eines Vierecks zerlegt man dieses am Besten geeignet in Teildreiecke.
Ist das Viereck konvex können wir folgenden Satz benutzen.

Satz 5518E (Flächeninhalt des Vierecks aus Länge der Diagonalen)

Seien ee und ff die Diagonalen eines konvexen Vierecks und φ\phi der Winkel dazwischen. Dann gilt für den Flächeninhalt des Vierecks
A=12⋅ef⋅sin⁡φA=\dfrac 1 2\cdot ef\cdot \sin\phi
 
 

Beweis

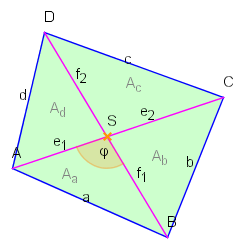
FlViereck.png
Die Bezeichnungen entnehme man nebenstehender Grafik.
Mit Formel 5518B erhalten wir als Fläche für die einzelnen Teildreiecke
Aa=12⋅e1⋅f1sin⁡φA_a=\dfrac {1} 2\cdot e_1 \cdot f_1 \sin \phi(1)
Ab=12⋅f1⋅e2sin⁡(180°−φ)A_b=\dfrac 1 2\cdot f_1 \cdot e_2 \sin (180°-\phi)(2)
Ac=12⋅e2⋅f2sin⁡φA_c=\dfrac {1} 2\cdot e_2 \cdot f_2 \sin \phi(3)
Ad=12⋅f2⋅e1sin⁡(180°−φ)A_d=\dfrac 1 2\cdot f_2 \cdot e_1 \sin (180°-\phi).(4)
Wegen sin⁡(180°−φ)=sin⁡φ\sin (180°-\phi)=\sin\phi können wir Gleichungen (2) und (4) als
Ab=12⋅f1⋅e2sin⁡φA_b=\dfrac 1 2\cdot f_1 \cdot e_2 \sin\phi(5)
und
Ad=12⋅f2⋅e1sin⁡φA_d=\dfrac 1 2\cdot f_2 \cdot e_1 \sin \phi.(6)
schreiben.
Addieren wir (1) und (6) sowie (2) und (5) ergeben sich
Aa+Ad=12⋅e1⋅(f1+f2)sin⁡φA_a+A_d=\dfrac 1 2\cdot e_1\cdot(f_1+f_2) \sin\phi(7)
Ab+Ac=12⋅e2⋅(f1+f2)sin⁡φA_b+A_c=\dfrac 1 2\cdot e_2\cdot(f_1+f_2) \sin\phi.(8)
Durch Addition der letzen beiden Gleichungen erhalten wir die Behauptung. □\qed

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie