Das Trapez
Das Trapez ist ein Viereck, in dem zwei Seiten parallel sind. Die parallelen Seiten heißen Grundseiten des Trapezes.
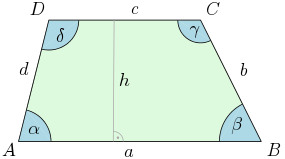
Abb. 1 zeigt die typische Benennung der Bestimmungsstücke eines Trapezes. Dabei sind und die parallelen Seiten. Eine der Grundseiten (meist die längere) heißt auch Basis. Die nicht parallelen Seiten werden Schenkel genannt.
Ein Trapez heißt gleichschenklig, wenn seine Schenkel (also und gleich lang sind).
Umfang
Für den Umfang des Trapezes gilt:
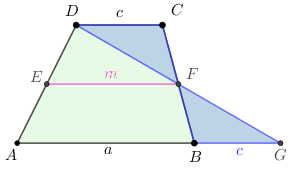
Abb. 2: Zur Ermittlung der Länge von .
Seien und sind die Mittelpunkte der Strecken bzw. (vgl. Abb. 2). Dann ist (Umkehrung des Strahlensatzes). Sei .
Die Dreiecke und sind kongruent, da die Strecken und gleich lang sind und die Winkel (Scheitelwinkel), sowie (Wechselwinkel). Damit gilt . Nach Strahlensatz gilt: , also
Flächeninhalt des Trapezes
Um den Flächeninhalt des Trapezes zu bestimmen, stellen wir fest, dass es flächengleich zum Dreieck aus Abb. 2 ist (wegen der Kongruenz der Dreiecke und ). Damit gilt:
.
Rechtwinkliges Trapez
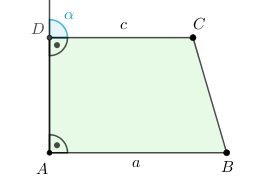
Abb. 3: Rechtwinkliges Trapez mit den beiden rechten Innenwinkeln
Ein Trapez heißt rechtwinklig (bzw. orthogonal), wenn es mindestens einen rechten Innenwinkel besitzt. Dann ist der Innenwinkel an der gegenüberliegenden parallelen Seite ebenfalls ein rechter Winkel. Denn die Winkel und sind Stufenwinkel an den parallelen Seiten und (siehe Abb. 3). Deshalb .
Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.
Michael Stifel
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе