Drachenviereck

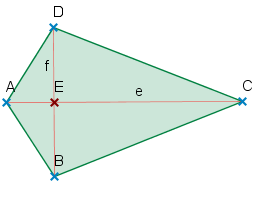
Deltoid.png
Ein Drachenviereck oder Deltoid ist ein ebenes Viereck,
oder (äquivalent)
  • das zwei Paare gleich langer benachbarter Seiten besitzt.
Oft wird nur die konvexe Form des Deltoids als Drachenviereck bezeichnet und die nicht-konvexe Form (mit einer konkaven Ecke AA in der Grafik) als Pfeilviereck.
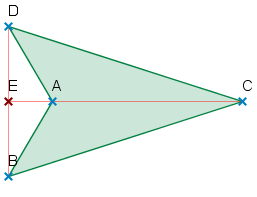
Deltoid2.png
(Die Bezeichnung "Drachenviereck" verweist auf die Form vieler Flugdrachen.)
Für jedes Deltoid gilt:
  • die Diagonalen stehen aufeinander senkrecht (sie sind orthogonal: das Deltoid ist ein orthodiagonales Viereck)
  • eine Diagonale halbiert die andere
  • zwei einander gegenüberliegende Winkel sind gleich
  • es hat einen Inkreis und ist daher ein Tangentenviereck.
Eine spezielles Drachenviereck ist der Rhombus (auch Raute): er ist ein gleichseitiges Deltoid.
Eine Verallgemeinerung des Drachenvierecks ist der (schräge) Drachen, bei dem nur verlangt wird, dass eine Diagonale durch die andere halbiert wird. Das Deltoid ist dann ein gerader Drachen.
Mit den Bezeichnungen der Figur gilt:
Die Diagonale AC‾\overline{AC} ist Symmetrieachse und halbiert die Diagonale BD‾\overline{BD}.
Sie teilt das Viereck ABCDABCD in zwei kongruente spiegelsymmetrische Dreiecke
(△ABC\triangle ABC und △ACD\triangle ACD).
Die Diagonale BD‾\overline{BD} teilt das Viereck in zwei gleichschenklige Dreiecke (△ABD\triangle ABD und △BCD\triangle BCD).
Die Innenwinkel bei BB und bei DD sind gleich groß.
Die Winkel bei AA und bei CC werden von der Diagonale halbiert.
Die Fläche AA eines Drachenvierecks lässt sich leicht aus den Längen der Diagonalen bestimmen:
A=AC‾⋅BD‾2=e⋅f2A = \dfrac{\overline{AC} \cdot \overline{BD}}{2} = \dfrac{e\cdot f}2
Der Umfang:
u=2⋅a+2⋅bu=2 \cdot a + 2 \cdot b
 
 

Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.

Karl Weierstraß

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Drachenviereck aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie