Flächeninhalt und Parallelogrammgleichung
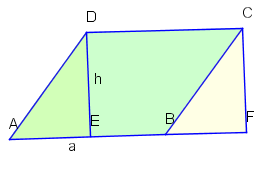
Zerlegung eines Parallelogramms in ein flächengleiches Rechteck
Durch Abschneiden des Dreieck und Ankleben an der anderen Seite überführen wir das Parallelogramm in ein flächengleiches Rechteck. Dieses hat den Flächeninhalt , welcher auch der Inhalt des Parallelogramms ist.
Formel 15WP (Flächeninhalt des Parallelogramms)
Der Flächeninhalt eines Parallelogramms ist das Produkt aus Grundseite mit der dazugehörigen Höhe.
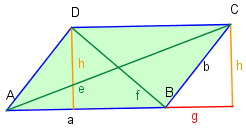
Formel 16GG (Parallelogrammgleichung)
Herleitung
Ein guter mathematischer Scherz ist immer besser als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen.
John Edensor Littlewood
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе