Satz des Pythagoras

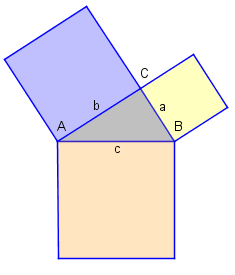
Pyth.png
Der Satz des Pythagoras stellt einen einfachen Zusammenhang zwischen den Seiten eines rechtwinkligen Dreiecks her.
In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse gleich der Summe der Quadrate über den Katheten.

Satz 16GD (Satz des Pythagoras)

In einem rechtwinkligen Dreieck seien mit cc die Hypotenuse (längste Seite) und mit aa und bb die beiden anderen Seiten (Katheten) bezeichnet. Dann gilt:
c2=a2+b2c^2 = a^2 + b^2
 
 
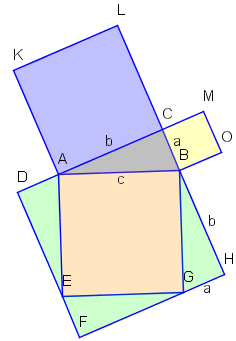
PythagorasB1.png

Beweis über Flächenzerlegung

Wir stellen fest, dass ΔABC\Delta ABC kongruent zu ΔBGH\Delta BGH ist. (Sie stimmen in den drei Seiten überein). Das gleiche gilt für die Dreiecke ΔADE\Delta ADE und ΔEFG\Delta EFG.
Der Flächeninhalt AVA_V des Vierecks CDFHCDFH ist AV=(a+b)2A_V = (a+b)^2; es gilt aber auch, dass AVA_V die Summe aus dem Flächeninhalt des Quadrates AEGBAEGB und dem Vierfachen des Flächeninhaltes des Dreiecks ΔABC\Delta ABC (AD=ab2 A_D = \dfrac{ab}{2}) ist. Damit erhalten wir: (a+b)2=c2+4⋅ab2(a+b)^2 = c^2 + 4\cdot \dfrac{ab}{2}. D.h. a2+b2+2ab=c2+2aba^2 + b^2 + 2ab = c^2 + 2ab und die Behauptung ergibt sich sofort. □\qed

Pythagoreische Tripel

Pythagoreische Tripel sind ganze Zahlen für die die Beziehung c2=a2+b2c^2=a^2+b^2 gilt. Einfachste Tripel ist 32+42=523^2+4^2=5^2. Mittels dieses pythagoreischen Zahlentripels kann man einen rechten Winkel konstruieren, indem man ein Dreieck mit den entsprechenden Seitenlängen auslegt.
Auf Grund seiner Bedeutung zeigen wir noch, dass wir den Satz des Pythagoras aus diversen anderen Beziehungen herleiten können.
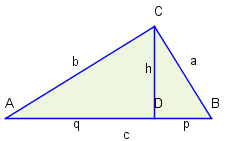
DreieckRwPq.png

Herleitung aus dem Kathetensatz

Nach dem Kathetensatz gilt a2=pca^2 = pc und b2=qcb^2 = qc.
Also: a2+b2=pc+qc=(p+q)c=c2a^2 + b^2 = pc + qc = (p+q)c = c^2.
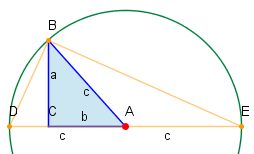
PythAusHs.png

Herleitung aus Höhensatz

Man konstruiert den Thaleskreis mit dem Mittelpunkt AA und dem Radius cc. Das Dreieck DEBDEB ist nach dem Satz des Thales rechtwinklig mit dem rechten Winkel bei BB und der Höhe a=BCa=BC. Man wende den Höhensatz an: a2=(c−b)(c+b)=c2−b2a^2=(c-b)(c+b)=c^2-b^2, woraus man sofort c2=a2+b2c^2=a^2+b^2 erhält.

Herleitung aus dem Kosinussatz

Der Cosinussatz für das allgemeine Dreieck lautet: c2=a2+b2−2ab⋅cos⁡γc^2 = a^2 + b^2 - 2ab\cdot \cos\gamma, wobei γ\gamma der von den Seiten aa und bb eingeschlossene Winkel ist.
Für γ=90°\gamma=90° ergibt sich der Pythagoras als Spezialfall sofort.

Herleitung aus dem Sinussatz

Laut Sinussatz gilt: sin⁡αa=sin⁡βb=sin⁡γc\dfrac {\sin\alpha}a = \dfrac {\sin\beta}b = \dfrac {\sin\gamma}c. Da γ=90°\gamma=90° ist, erhalten wir: sin⁡αa=sin⁡βb=1c\dfrac {\sin\alpha}a = \dfrac {\sin\beta}b = \dfrac {1}c. Etwas umgeformt ergeben sich: a=c⋅sin⁡αa=c\cdot \sin\alpha und b=c⋅sin⁡βb=c\cdot \sin\beta.
Natürlich kann man dieses Beziehungen auch gleich durch Anwendung der Definition des Sinus erhalten.
Jedenfalls ist a2+b2=c2(sin⁡2α+sin⁡2β)a^2+b^2=c^2(\sin^2\alpha+\sin^2\beta). Womit uns nur noch zu zeigen bleibt, dass sin⁡2α+sin⁡2β=1\sin^2\alpha+\sin^2\beta=1
Wir wissen: sin⁡β=sin⁡(90°−α)=cos⁡α\sin\beta= \sin(90°-\alpha)=\cos\alpha und mit sin⁡2α+cos⁡2α=1\sin^2\alpha+\cos^2\alpha=1 ergibt sich die Behauptung.
Bei dieser Herleitung haben wir etwas gemogelt. In der Regel steckt in der Beziehung sin⁡2α+cos⁡2α=1\sin^2\alpha+\cos^2\alpha=1 schon der Satz des Pythagoras, den wir hier ja erst beweisen wollen.

Mit dem Satz des Pythagoras wissen wir, dass für die Seitenlängen die Gleichung c2=a2+b2c^2=a^2+b^2 gilt. Man kann nun natürlich fragen, ob dies hinreichend ist um rechtwinklige Dreieck zu charakterisieren. Die Antwort darauf liefert der folgende Satz:

Satz (Umkehrung des Satzes des Pythagoras)

Gilt in einem Dreieck c2=a2+b2c^2=a^2+b^2, so ist dieses Dreieck rechtwinklig mit der Hypotenuse cc.

Beweis

Im Dreieck △ABC\triangle ABC gelte c2=a2+b2c^2=a^2+b^2. Sei △A′B′C′\triangle A'B'C' ein beliebiges rechtwinkliges Dreieck für das gilt ∣A′C′∣=b|A'C'|=b und ∣B′C′∣=a|B'C'|=a. In diesem Dreieck gilt der Satz des Pythagoras: ∣A′B′∣2=∣A′C′∣2+∣B′C′∣2|A'B'|^2=|A'C'|^2+|B'C'|^2 =a2+b2=a^2+b^2. Wegen c2=a2+b2c^2=a^2+b^2 ist c2=∣A′B′∣2c^2=|A'B'|^2, also c=∣A′B′∣c=|A'B'|. Damit stimmen die Dreiecke △ABC\triangle ABC und △A′B′C′\triangle A'B'C' in allen drei Seiten überein und sind kongruent. Dann muss △ABC\triangle ABC aber rechtwinklig sein. □\qed

Beispiel

Die sogenannte Zwölfknotenschnur ist ein einfaches Werkzeug, mit dessen Hilfe rechte Winkel bestimmt wurden. Dazu wurde eine Schnur durch elf Knoten in zwölf gleiche Teile geteilt. Legt man diese nun zu einem Dreieck, wobei die Seiten das Verhältnis 3:4:53:4:5 aufweisen, dann erfüllen sie die Gleichung (3x)2+(4x)2=(5x)2(3x)^2+(4x)^2=(5x)^2, wobei xx die Länge der Teile ist. Dieses Dreieck ist damit nach der Umkehrung des Satzes des Pythagoras ein rechtwinkliges Dreieck.

Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.

Karl Menger

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Spezielle Dreiecke