Kosinussatz
Andere Schreibweise: Cosinussatz.
Satz 5330N (Kosinussatz)
In einem beliebigen Dreieck gilt:
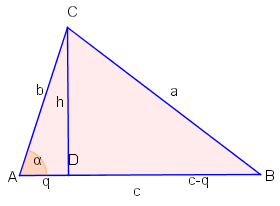
Beweis
Mit der Definition des Kosinus haben wir und umgestellt zu: . Setzen wir dies in (2) ein, ergibt sich die Behauptung:
.
Die anderen Fälle erhält man durch analoge Überlegungen mit den anderen Seiten und Winkeln.
Mit dem Kosinussatz kann man bei zwei gegebenen Seiten und dem eingeschlossenen Winkel die dritte Seite berechnen.
So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.
Bertrand Russell
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе