Innenwinkel im Dreieck

Die Innenwinkel eines Dreiecks sind die Winkel, deren Scheitelpunkte die Ecken sind.

Satz 5515C (Innenwinkelsatz im Dreieck)

In einem Dreieck beträgt die Summe der Innenwinkel 180°.
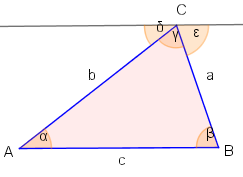
InnenwinkelSatz.png
Sind α\alpha, β\beta und γ\gamma die Innenwinkel eines Dreiecks, so gilt:
α+β+γ=180°\alpha + \beta + \gamma =180°.

Beweis

Zum Beweis benutzen wir den Wechselwinkelsatz.
Zur Seite AB‾\overline {AB} bilden wir die Parallele durch den Punkt CC. Dann ist der Winkel δ\delta Wechselwinkel zu α\alpha und ϵ\epsilon Wechselwinkel zu β\beta. Damit gilt α=δ\alpha = \delta und β=ϵ\beta = \epsilon. Zusammen mit γ\gamma ergänzen sie sich zu 180°. □\qed

Anwendung und Folgerungen

Nach dem Innenwinkelsatz kann es keine Dreiecke mit Winkeln ≥180°\geq 180° geben und ein Dreieck kann maximal einen stumpfen Winkel haben.
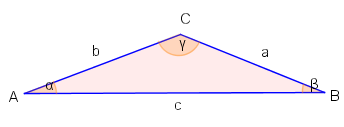
DreieckStumpf.png
Sind zwei Winkel gegeben, so ist der dritte eindeutig bestimmt.
Unter diesen Voraussetzungen sind folgende Winkelkombinationen im Dreieck möglich:
 
 

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie