Dreiecksungleichung

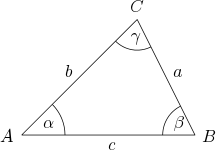
Dreieck.png
In jedem Dreieck ist die Summe zweier Seitenlängen größer als die Dritte.
Sind die Seiten aa, bb und cc so gilt also:
a+b>ca+b>c; a+c>ba+c>b; b+c>ab+c>a
Anschaulich ergibt sich die Gültigkeit der Gleichung aus der Eigenschaft einer Strecke, die kürzeste Verbindung zweier Punkte zu sein.

Anwendung

Die Dreiecksungleichung hilft schnell zu entscheiden, ob bei gegebenen Seitenlängen ein Dreieck konstruierbar ist.
Man kann z.B. kein Dreieck mit den Seitenlängen 2cm, 3cm und 6cm konstruieren, da die Dreiecksungleichung verletzt wäre.
 
 

Herleitung aus dem Cosinussatz

Die Stücke des Dreiecks seien wie üblich bezeichnet.
Es gilt nach Definition des Kosinus für beliebiges γ\gamma:
−1≤cos⁡γ≤1-1\leq\cos\gamma\leq1,
also
0≤1+cos⁡γ0\leq 1+\cos\gamma.
Nach Multiplikation mit 2ab2ab:
0≤2ab(1+cos⁡γ)=2ab+2abcos⁡γ0\leq 2ab(1+\cos\gamma)=2ab+2ab\cos\gamma.(1)
Der Kosinussatz ergibt sich mit
c2=a2+b2−2abcos⁡γc^2=a^2+b^2-2ab\cos\gamma
Addieren wir zur Ungleichung (1) diese Gleichung, erhalten wir
c2≤a2+b2−2abcos⁡γ+2ab+2abcos⁡γ=a2+b2+2abc^2\leq a^2+b^2-2ab\cos\gamma+2ab+2ab\cos\gamma=a^2+b^2+2ab.
Nach Anwendung der entsprechenden binomischen Formel:
c2≤(a+b)2c^2\leq (a+b)^2,(2)
und nach dem Wurzelziehen ergibt sich die Behauptung. Für die anderen Seiten kann man analog rechnen. Die Gleichheit kann in (2) nur dann auftreten, wenn γ=180°\gamma=180° gilt, ein Fall, der in einem Dreieck aber nicht vorkommen kann. □\qed

Eine mathematische Wahrheit ist an sich weder einfach noch kompliziert, sie ist.

Émile Lemoine

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie