Binomische Formeln
Als binomische Formeln werden üblicherweise die folgenden drei Umformungen bezeichnet:
Erste binomische Formel (Plus-Formel)
Zweite binomische Formel (Minus-Formel)
Dritte binomische Formel (Plus-Minus-Formel)
Beweis
Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen: 1) 2) 3)
Geometrische Veranschaulichung
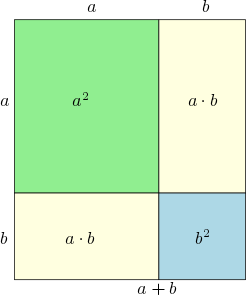
Das nebenstehende mehrfarbige Quadrat hat die Seitenlänge . Wie sofort ersichtlich ist, passen die zwei Quadrate und hinein, und es bleiben zwei Rechtecke mit jeweils dem Flächeninhalt übrig. Dadurch ergibt sich .
Eine Veranschaulichung der dritten binomischen Formel erhält man durch folgende [!Zerlegung] eines Quadrats der Seitenlänge in zwei kongruente Trapeze:

Veranschaulichung der dritten binomischen Formel
Anwendungen
Tricks zum Kopfrechnen
Diese Formeln, häufig in der Mathematik benutzt, bieten auch eine Hilfe beim Kopfrechnen. Das Quadrat einer beliebigen Zahl zwischen 10 und 100 lässt sich oft einfach mit der binomischen Formel bestimmen, indem man die Berechnung auf Quadrate von einfacheren Zahlen (Vielfache von 10 oder einstellige Zahlen) zurückführt. Beispielsweise ist
oder
- .
Bei Kenntnis der Quadratzahlen bis 20 lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist
- .
Mit Hilfe der binomischen Formeln lassen sich Multiplikation und Division auf die einfacheren Rechenarten Quadrieren, Addieren, Subtrahieren, Halbieren und Verdoppeln zurückführen:
Wer an Stelle des Einmaleins die ersten hundert Quadratzahlen kennt, kann so das allgemeine Produkt zweier Zahlen leicht berechnen.
Addition und Subtraktion von Wurzeln
Die erste und zweite binomische Formel liefern auch ein Rechenverfahren zur Addition bzw. Subtraktion von Wurzeln. Da bzw. nicht direkt berechenbar sind, quadriert man die Summe bzw. Differenz und zieht anschließend aus dem Quadrat die Wurzel. Das Verfahren führt aber zu Schachtelwurzeln, die nicht unbedingt einfacher sind als die ursprünglichen Ausdrücke.
Da Wurzeln als nichtnegativ definiert und Quadrate von sich aus nie negativ sind, ist bei Differenzen von Wurzeln eine Fallunterscheidung nötig:
- für
- für
Erweiterungen auf mehrgliedrige Ausdrücke
Eine Verallgemeinerung der binomischen Formeln auf Potenzen von Polynomen, also von Summen mit mehr als zwei Gliedern, führt auf das Multinomialtheorem. Beispielsweise gilt für das Quadrat eines Trinoms
- .
Die Koeffizienten sind in der Pascalschen Pyramide enthalten. So ist
Beispielanwendung
So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.
Ernst Mach
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Binomische Formeln
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе