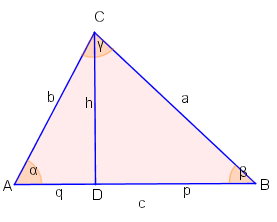
Projektionssatz

In einem beliebigen Dreieck gilt:
c=a⋅cos⁡ β+b⋅cos⁡ αc=a\cdot\cos \, \beta+b\cdot\cos \, \alpha
b=c⋅cos⁡ α+a⋅cos⁡ γb=c\cdot\cos \, \alpha+a\cdot\cos \, \gamma
a=c⋅cos⁡ β+b⋅cos⁡ αa=c\cdot\cos \, \beta+b\cdot\cos \, \alpha

Beweis

DreieckH.png
Es reicht eine der Formeln zu beweisen; die anderen ergeben sich durch zyklisches Vertauschen der Seiten und Winkel.
Wir zeichnen die Höhe von CC auf Seite cc. Es gilt
∠DCA=90°−α\angle DCA = 90°-\alpha
und
∠BCD=90°−β\angle BCD = 90°-\beta.
Jetzt wenden wir die Definition des Sinus an:
sin⁡(90°−α)=qb\sin(90°-\alpha)= \dfrac{q}{b} und sin⁡(90°−β)=pa\sin(90°-\beta)= \dfrac{p}{a}.
Nach Satz 5220B gilt: sin⁡(90°−φ)=cos⁡φ\sin(90°-\phi)= \cos\phi und damit erhalten wir:
cos⁡α=qb\cos\alpha= \dfrac{q}{b} und cos⁡β=pa\cos\beta= \dfrac{p}{a}.
Umgestellt erhalten wir:
p=a⋅cos⁡βp=a\cdot\cos\beta und q=b⋅cos⁡αq=b\cdot\cos\alpha.
In der Summe ergibt sich dann die Behauptung:
p+q=c=a⋅cos⁡β+b⋅cos⁡αp+q=c=a\cdot\cos\beta+b\cdot\cos\alpha. □\qed
 
 

Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.

Michael Stifel

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck