Die Mollweideschen Formeln

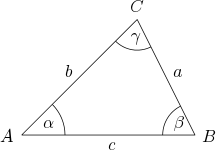
In einem beliebigen Dreieck gelten die nach Carl Brandan Mollweide benannten Formeln:

Satz 168F (Formeln von Mollweide)

b+ca=cos⁡β−γ2sin⁡α2\dfrac{b+c}{a} = \dfrac{\cos \dfrac{\beta -\gamma }{2} } {\sin \dfrac{\alpha }{2}} c+ab=cos⁡γ−α2sin⁡β2\dfrac{c+a}{b} = \dfrac{\cos \dfrac{\gamma -\alpha }{2} } {\sin \dfrac{\beta }{2}} a+bc=cos⁡α−β2sin⁡γ2\dfrac{a+b}{c} = \dfrac{\cos \dfrac{\alpha -\beta }{2} } {\sin \dfrac{\gamma }{2}}
b−ca=sin⁡β−γ2cos⁡α2\dfrac{b-c}{a} = \dfrac{\sin \dfrac{\beta -\gamma }{2} } {\cos \dfrac{\alpha }{2}} c−ab=sin⁡γ−α2cos⁡β2\dfrac{c-a}{b} = \dfrac{\sin \dfrac{\gamma -\alpha }{2} } {\cos \dfrac{\beta }{2}} a−bc=sin⁡α−β2cos⁡γ2\dfrac{a-b}{c} = \dfrac{\sin \dfrac{\alpha -\beta }{2} } {\cos \dfrac{\gamma }{2}}

Beweis

Dreieck.png
Zur Herleitung der Formeln benutzen wir den Sinussatz ac=sin⁡αsin⁡γ\dfrac a c =\dfrac {\sin\alpha}{\sin\gamma} und bc=sin⁡βsin⁡γ\dfrac b c =\dfrac {\sin\beta}{\sin\gamma}.
a+bc=sin⁡α+sin⁡βsin⁡γ\dfrac {a+b} c =\dfrac{\sin\alpha+\sin\beta}{\sin\gamma}
=sin⁡α+sin⁡β2sin⁡γ2cos⁡γ2=\dfrac{\sin\alpha+\sin\beta}{2\sin\dfrac \gamma 2\cos\dfrac \gamma 2} (Satz 5220A)
=sin⁡α+β2cos⁡α−β2sin⁡γ2cos⁡γ2=\dfrac{\sin\dfrac {\alpha+\beta} 2 \cos\dfrac {\alpha-\beta} 2}{\sin\dfrac \gamma 2\cos\dfrac \gamma 2} (Satz 5316D)
=cos⁡α−β2sin⁡γ2= \dfrac{\cos \dfrac{\alpha -\beta }{2} } {\sin \dfrac{\gamma }{2}} (wegen cos⁡γ2=cos⁡(π2−α+β2)=sin⁡α+β2\cos \dfrac \gamma 2=\cos\braceNT{\dfrac \pi 2-\dfrac {\alpha+\beta} 2}=\sin\dfrac {\alpha+\beta} 2 vgl. Satz 5220B)
Die anderen Formeln ergeben sich durch zyklisches Vertauschen der Seiten und Winkel und analoge Schlussweisen. □\qed
Nach Division der entsprechenden Gleichungen und unter Benutzung von cos⁡γ2=sin⁡α+β2\cos \dfrac \gamma 2=\sin\dfrac {\alpha+\beta} 2, erhält man die Folgerung:

Nepersche Gleichungen

a−ba+b=tan⁡α−β2tan⁡α+β2\dfrac {a-b} {a+b}=\dfrac {\tan \dfrac {\alpha-\beta} 2} {\tan \dfrac {\alpha+\beta} 2} b−cb+c=tan⁡β−γ2tan⁡β+γ2\dfrac {b-c} {b+c}=\dfrac {\tan \dfrac {\beta-\gamma} 2} {\tan \dfrac {\beta+\gamma} 2} c−ac+a=tan⁡γ−α2tan⁡γ+α2\dfrac {c-a} {c+a}=\dfrac {\tan \dfrac {\gamma-\alpha} 2} {\tan \dfrac {\gamma+\alpha} 2}
 
 

In der Mathematik gibt es keine Autoritäten. Das einzige Argument für die Wahrheit ist der Beweis.

K. Urbanik

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck