Sinussatz

Satz 5330M (Sinussatz)

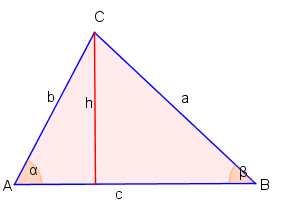
SinS1.png
In einem beliebigen Dreieck gilt:
sin⁡αa = sin⁡βb = sin⁡γc\dfrac {\sin\alpha}a \, =\, \dfrac {\sin\beta}b \, =\, \dfrac {\sin\gamma}c

Beweis

Die Herleitung des Sinussatzes beruht auf der Definition des Sinus, wobei die dafür notwendigen rechtwinkligen Dreiecke durch Einzeichnen der Höhen erzeugt werden.
Wir zeichnen die Höhe von CC auf Seite cc und wenden die Definition des Sinus an.
Danach gilt einerseits: sin⁡α=hb\sin\alpha=\dfrac h b und andererseits: sin⁡β=ha\sin\beta=\dfrac h a. Nach hh umgestellt: h=b⋅sin⁡αh=b\cdot \sin\alpha und h=a⋅sin⁡βh=a\cdot \sin\beta, also: b⋅sin⁡α=a⋅sin⁡βb\cdot \sin\alpha=a\cdot \sin\beta.
Und wir erhalten: sin⁡αa=sin⁡βb\dfrac {\sin\alpha}a = \dfrac {\sin\beta}b.
Unter Benutzung der gleichen Schlussweise bei einer weiteren Höhe erhalten wir die vollständige Behauptung.
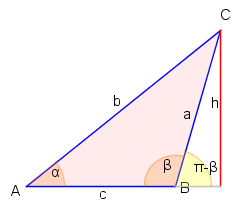
SinS2.png
Sinussatz im stumpfwinkligen Dreieck
Beim Beweis waren wir bisher von einem spitzwinkligen Dreieck ausgegangen. Im rechtwinkligen Dreieck fallen Höhe und Dreiecksseite zusammen und sin⁡90°=1\sin 90°=1, sodass der Satz trivial gilt.
Im stumpfwinkligen Dreieck (siehe Grafik) ergibt sich sin⁡α=hb\sin\alpha=\dfrac h b und sin⁡(π−β)=ha\sin(\pi-\beta)=\dfrac h a. Da nach Satz 5220A sin⁡(π−β)=sin⁡β\sin(\pi-\beta)=\sin\beta ergibt sich die Behauptung wie im ersten Teil des Beweises. □\qed
 
 

Bemerkungen

Bezeichnen wir mit rr den Radius des Umkreises, so gilt nach Satz 5515F
2r=asin⁡α=bsin⁡β=csin⁡γ2r=\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}

Die Mathematik als Fachgebiet ist so ernst, daß man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.

Blaise Pascal

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck