Beispiel zum Sinussatz

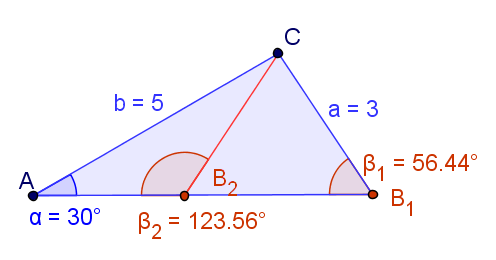
SiSatzBsp.png
Das folgende Beispiel soll Problematik der Berechnung von fehlenden Winkeln mit Hilfe des Sinussatzes verdeutlichen.
Seien zwei Seiten mit den Längen a=3a=3 und b=5b=5 gegeben, sowie der Winkel α=30°\alpha=30°. Dann ergibt sich:
sin⁡βsin⁡α=ba\dfrac{ \sin \beta}{\sin\alpha}=\dfrac b a, also sin⁡β1/2=53\dfrac { \sin \beta} {1/2}=\dfrac 5 3
sin⁡β=56≈0,8333\sin \beta=\dfrac 5 6 \approx 0,8333
Wegen der Eigenschaften der Sinusfunktion gibt es für den Winkel β\beta jetzt 2 Lösungen.
β1≈56,44°\beta_1\approx 56,44° und β2≈123,56°\beta_2\approx 123,56°.
Beide Winkel ergänzen sich zu 180°180° und liefern gültige Dreiecke, wie man in der obigen Abbildung sehen kann.
Ist der gegebene Winkel α≥90°\alpha\ge 90°, so wird die Lösung wieder eindeutig, da nur der kleinere der beiden β\beta-Winkel zu einem gültigen Dreieck führt, der andere ist immer größer als 90°90°, was wegen α≥90°\alpha\ge 90° zu einer Verletzung Innenwinkelsatzes führt. Ein Dreieck kann keine zwei stumpfen Winkel besitzen.
 
 

Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.

Karl Weierstraß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Trigonometrische Sätze