Mittelsenkrechte und Umkreis im Dreieck

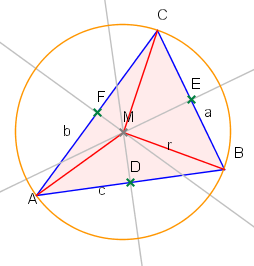
DreieckMittelsenkrechte.png
Bildet man in einem Dreieck von jeder Seite den Mittelpunkt und errichtet darauf ein Senkrechte, so erhält man die Mittelsenkrechten des Dreiecks

Satz 5515E (Mittelsenkrechten im Dreieck)

Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Umkreises (des Kreises, auf dem die Eckpunkte des Dreiecks liegen).
 
 

Beweis

Sei DD der Mittelpunkt der Seite AB‾\overline{AB}. Jeder Punkt auf der Mittelsenkrechte durch DD ist gleich weit von AA und BB entfernt.
Analoges gilt für die Punkte auf der Mittelsenkrechte durch EE im Verhältnis zu den Punkten BB und CC.
Der Schnittpunkt MM beider Mittelsenkrechten ist damit gleich weit von allen Ecken des Dreiecks entfernt; damit ist er Mittelpunkt eines Kreises durch die drei Ecken, des Umkreises.
MM hat den gleichen Abstand von AA und CC, damit muss aber die Gerade durch MM und FF senkrecht auf der Seite AB‾\overline{AB} stehen, also eine Mittelsenkrechte sein. Womit gezeigt ist, dass sich die Mittelsenkrechten in einem Punkt schneiden.□\qed
Ist das Dreieck spitzwinklig liegt der Schnittpunkt innerhalb, bei einem stumpfwinkligen Dreieck außerhalb des Dreiecks. In einem rechtwinkligen Dreieck halbiert der Mittelpunkt des Umkreises die Hypotenuse (vgl. Satz des Thales).

Satz 5515F (Umkreisradius)

Für den Umkreisradius rr gilt:
2r=asin⁡α=bsin⁡β=csin⁡γ2r=\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}.

Beweis

Sei α1=∠BAM=∠MBA\alpha_1=\angle BAM=\angle MBA . Dann ist ∠MBC=∠BCM=β−α1\angle MBC=\angle BCM=\beta-\alpha_1 und weiter ist dann ∠MCA=∠CAM=γ−(β−α1)=γ−β+α1\angle MCA=\angle CAM= \gamma-(\beta-\alpha_1)=\gamma-\beta+\alpha_1. Es gilt außerdem α=∠CAM+∠BAM\alpha=\angle CAM +\angle BAM; also α=α1+γ−β+α1\alpha=\alpha_1+\gamma-\beta+\alpha_1 und auch α+β−γ=2α1\alpha+\beta-\gamma=2\alpha_1 und 180°−2γ=2α1180°-2\gamma=2\alpha_1, womit wir letztlich α1=90°−γ\alpha_1=90°-\gamma erhalten.
Betrachten wir das rechtwinklige Dreieck ΔADM\Delta ADM so können wir herleiten: sin⁡γ=cos⁡(90°−γ)\sin\gamma=\cos(90°-\gamma) =cos⁡α1=\cos\alpha_1 =c/2r=c2r=\dfrac{c/2}{r}=\dfrac{c}{2r}, womit wir die Behauptung erhalten.
Analog kann der Beweis für die anderen Seiten und Winkel geführt werden. □\qed

Die beste von allen Sprachen der Welt ist eine künstliche Sprache, eine ziemlich gedrängte Sprache, die Sprache der Mathematik.

N. I. Lobatschewski

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck