Ankreise

Für jedes Dreieck existieren genau drei Kreise, die jeweils eine Dreiecksseite im Inneren und von den beiden anderen Seiten die Verlängerungen berühren. Diese drei Kreise heißen die Ankreise des Dreiecks. Die Ankreismittelpunkte liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der beiden Außenwinkel, die nicht zu dem Innenwinkel gehören.

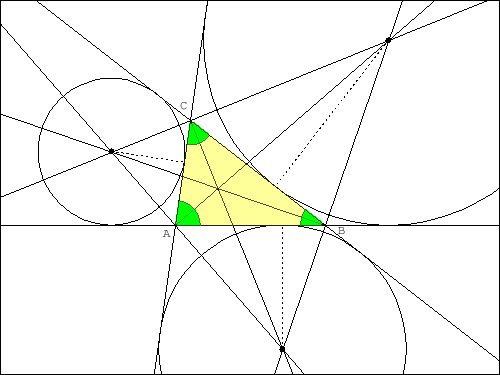
Der Radius desjenigen Ankreises, der die Seite [BC] im Inneren berührt, ergibt sich aus $\varrho_a = \dfrac{2 F}{b+c-a}$, wobei $F$ der Flächeninhalt des Dreiecks ist. Analog berechnen sich die Radien $\varrho_b$ und $\varrho_c$ der beiden anderen Ankreise.

Die Ankreismittelpunkte des Dreiecks ABC bilden ein Dreieck, dessen Höhenschnittpunkt der Inkreismittelpunkt des Dreiecks ABC ist.

Der Nagel-Punkt, benannt nach dem deutschen Mathematiker Christian Heinrich von Nagel (1803-1882), gehört zu den besonderen Punkten eines Dreiecks. Für ein gegebenes Dreieck ABC betrachtet man die Punkte D, E und F, in denen die Ankreise die Seiten des Dreiecks berühren. Verbindet man diese Berührpunkte mit den gegenüber liegenden Ecken des Dreiecks (also mit A, B bzw. C), so schneiden sich diese Verbindungsstrecken in einem Punkt N. Dieser wird als Nagel-Punkt des Dreiecks bezeichnet.

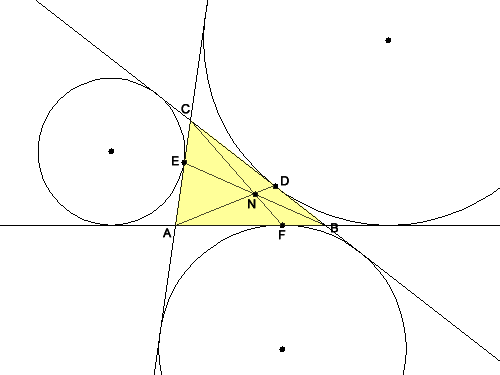
Betrachtet man außer dem Nagel-Punkt N des Dreiecks ABC auch den Inkreismittelpunkt I und den Schwerpunkt S, dann liegen die Punkte N, S und I auf einer Geraden, und es gilt $\overline{NS} : \overline{SI} = 2 : 1$, wobei der Schwerpunkt S zwischen den Punkten N und I liegt. In dieser Eigenschaft weist die Gerade durch die Punkte N, S und I eine Analogie zur Eulerschen Gerade auf.