Eulersche Gerade
Unter der eulerschen Geraden (oder kurz Eulergeraden) eines Dreiecks (benannt nach dem Mathematiker Leonhard Euler) versteht man die Gerade, die durch den Schwerpunkt, den Umkreismittelpunkt und den Höhenschnittpunkt des Dreiecks geht.
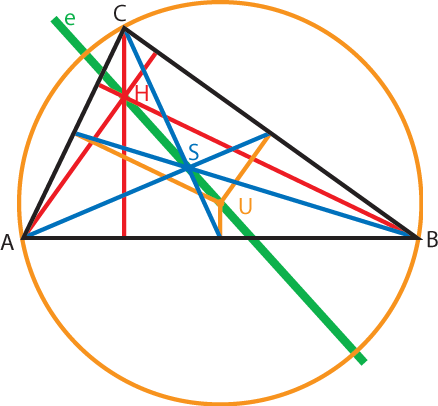
Falls das Dreieck mit bezeichnet wird, dann liegen also sein Schwerpunkt , sein Umkreismittelpunkt und sein Höhenschnittpunkt auf einer Geraden. Außerdem gilt , wobei der Punkt zwischen den Punkten und liegt. Die eulersche Gerade geht auch durch den Mittelpunkt des Feuerbachkreises; der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke .
Auf der eulerschen Geraden des Dreiecks liegt auch der Umkreismittelpunkt des Dreiecks, das von den Tangenten an den Umkreis des Dreiecks in den Punkten und gebildet wird. Darüber hinaus enthält die eulersche Gerade noch weitere Punkte mit interessanten Eigenschaften.
Es sei angemerkt, dass man im Falle eines gleichseitigen Dreiecks nicht mehr von der eulerschen Geraden sprechen kann, weil dann die drei bestimmenden Punkte und zu einem Punkt zusammenfallen. (Sie liegen dann auf unendlich vielen Geraden, d.h. jede Gerade durch diesen einen Punkt könnte als eulersche Gerade aufgefasst werden, was wir aber der Eindeutigkeit halber vermeiden.)
Man darf nicht das, was uns unwahrscheinlich und unnatürlich erscheint, mit dem verwechseln, was absolut unmöglich ist.
Carl Friedrich Gauß
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Eulersche Gerade
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе