Simsonsche Gerade

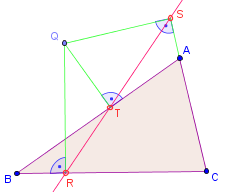
Simson.png
Liegen die Fußpunkte eines Punktes QQ auf die (eventuell verlängerten) Seiten eines Dreiecks △ABC\triangle ABC auf einer gemeinsamen Geraden, so wird diese Gerade als simsonsche Gerade und der Punkt QQ als ihr Pol bezeichnet.

Satz A7S9 (Simsongerade und Umkreis)

Die Fußpunkte der aus einem Punkt QQ auf die Dreiecksseiten gefällten Lote liegen genau dann auf einer Geraden, wenn QQ auf dem Umkreis des Dreiecks liegt.
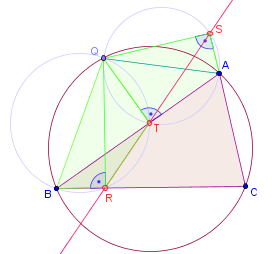
Simson1.png

Beweis

Unabhängig von der Lage von QQ auf dem Umkreis von △ABC\triangle ABC stellen wir fest: 1) Das Viereck QTASQTAS ist ein Sehnenviereck (da die gegenüberliegende Winkel sind bei SS und TT 90° sind und Anwendung von Satz 5513A). 2) Ebenso ist das Viereck QBRTQBRT ein Sehnenviereck, denn △QBR\triangle QBR und △QBT\triangle QBT sind rechtwinklig und daher liegen alle vier Punkte auf dem gleichen Thaleskreis. "⇐\Leftarrow": ∠ATS=∠AQS\angle ATS=\angle AQS (da beide Peripheriewinkel über der Sehne AS‾\ovl{AS} sind) =90°−∠QAS=90°-\angle QAS =∠QAC−90°=\angle QAC-90° =90°−∠QBC=90°-\angle QBC ,da ∠QAC+∠QBC=180°\angle QAC+\angle QBC=180° =∠BQR=\angle BQR (da △BRQ\triangle BRQ rechtwinklig ist) =∠BTR=\angle BTR (Peripheriewinkel über der Sehne BR‾\ovl {BR}).
Damit kann man sich leicht überlegen, dass ∠RTS=180°\angle RTS=180° und daher liegen die drei Punkte auf einer Geraden.
"  ⟹  \implies": Da QTASQTAS und QBRTQBRT Sehnenvierecke sind, gilt: ∠BQR=∠BTR\angle BQR=\angle BTR =∠ATS=∠AQS=\angle ATS=\angle AQS . Also ∠QBR=∠QAS\angle QBR=\angle QAS und damit ist QBCAQBCA ein Sehnenviereck, daher liegt QQ auf dem Umkreis. □\qed
 
 

Satz A7SC

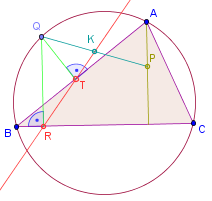
Shalb.png
Liegen QQ auf dem Umkreis des Dreiecks △ABC\triangle ABC. Dann halbiert die Simsongerade die Verbindungsstrecke zwischen QQ und dem Höhenschnittpunkt PP.

Beweis

Sei KK der Schnittpunkt der Simsongerade mit der Verbindungsstrecke QPQP. Die Höhe durch AA schneide BC‾\ovl {BC} in LL und den Umkreis in HH. QH‾\ovl {QH} schneide BC‾\ovl {BC} in NN und die Simsongerade in MM.
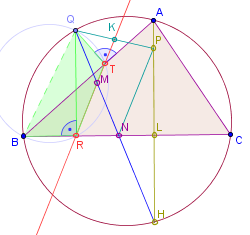
Shalb1.png
Das Viereck QBRTQBRT ist ein Sehnenviereck (siehe Beweis von Satz A7S9), damit gilt ∠QRT=∠QBT\angle QRT=\angle QBT =∠QHA=\angle QHA (da Peripheriewinkel über Sehne QA‾\ovl {QA}) =∠HQR=\angle HQR, da AH‾ ∣∣ QR‾\ovl {AH}\, ||\, \ovl {QR} und Wechselwinkel, damit gilt ∣QM‾∣=∣MR‾∣|\ovl{QM}|=|\ovl{MR}|. Da △QRN\triangle QRN rechtwinklig ist, gilt ∠MRN=90°−∠QRM\angle MRN=90°-\angle QRM und ∠RNM=90°−∠RQM\angle RNM=90°-\angle RQM, also auch
∠MRN=∠RNM\angle MRN=\angle RNM(1)
∠MRN=∠RNM\angle MRN=\angle RNM, daher ∣MR‾∣=∣MN‾∣|\ovl{MR}|=|\ovl{MN}|, womit gilt
∣QM‾∣=∣MN‾∣|\ovl{QM}|=|\ovl{MN}|,(2)
und MM ist der Mittelpunkt von QN‾\ovl {QN}.
Nach Satz A7RF gilt ∣PL‾∣=∣LH‾∣|\ovl{PL}|=|\ovl{LH}|, die Dreiecke △PNL\triangle PNL und △HNL\triangle HNL sind also kongruent (sie stimmen in 2 Seiten und dem eingeschlossenen rechten Winkel überein). Also: ∠PNL=∠LNH\angle PNL=\angle LNH =∠RNM=\angle RNM (Scheitelwinkel) =∠MRN=\angle MRN (nach (1)) Damit sind PN‾\ovl {PN} und RT‾\ovl {RT} parallel. Mit dem Strahlensatz (Zentrum in QQ) gilt dann:
∣QK‾∣∣KP‾∣=∣QM‾∣∣MN‾∣\dfrac{|\ovl{QK}|}{|\ovl{KP}|}=\dfrac{|\ovl{QM}|}{|\ovl{MN}|},
und wegen (2) erhalten wir
∣QK‾∣=∣KP‾∣|\ovl{QK}|=|\ovl{KP}|. □\qed

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck