Der Feuerbachkreis
Satz A7RA (Feuerbachkreis)
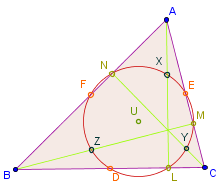
Der Feuerbachkreis
Die Mittelpunkte der Seiten (, und ) eines Dreiecks, die Fußpunkte der Höhen des Dreiecks (, und ) und die Mittelpunkte der drei Verbindungsstrecken des Höhenschnittpunkts mit den Eckpunkten des Dreiecks (, und ) liegen auf einem Kreis, dem Feuerbachkreis oder Neun-Punkte-Kreis.
Beweis
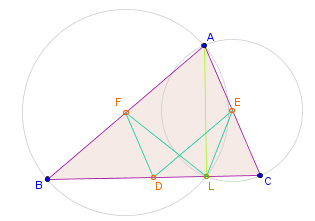
Wir verbinden die Punkte wie in Bild 1. Da das Dreieck rechtwinklig ist, ist nach dem Satz des Thales der Mittelpunkt des Thaleskreises. Nach dem Peripheriewinkelsatz gilt: . Analog ergibt sich im Dreieck dann . Damit: . Nach Satz A7RB ist ein Parallelogramm, also gilt . Nach Satz A7RC liegen die Punkte , , und auf einem Kreis. Analog kann man erschließen, dass und auf ebene diesem Kreis liegen.
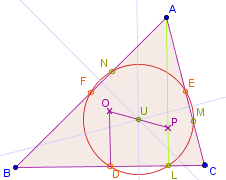
Wegen dieser Peripheriewinkelbeziehung liegt der Mittelpunkt des Kreises auf den Mittelsenkrechten der Strecken , und (vgl. Bild 2). Sind nun der Höhenschnittpunkt und der Schnittpunkt der Mittelsenkrechten, so halbiert die Strecke . (Parallelverschiebung von bis und deckungsgleich sind und Anwenden des Strahlensatzes.)
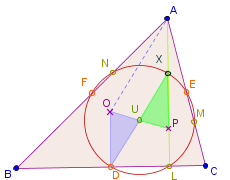
Sei nun der Schnittpunkt der Geraden durch und mit der Höhe . Die beiden Dreiecke und sind kongruent. (Sie stimmen in den Seiten und überein und allen Winkeln, da diese Scheitelwinkel bzw. Wechselwinkel sind.) Damit ist und liegt auf dem Kreis durch , , , , und . Nach Satz 5515G ist und wegen der Kongruenz von und gilt somit . Ähnlich zeigt man, dass der Kreis durch die Punkte und geht.
ist ein Parallelogramm ( und sind parallel und gleichlang, entsteht durch Parallelverschiebung von .) Es gilt: .
An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.
Godfrey Harold Hardy
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе