Satz von Menelaos

Der Satz von Menelaos macht eine Aussage über Geraden, die Dreiecke schneiden.
MenelaosSatz.png

Satz (Satz von Menelaos)

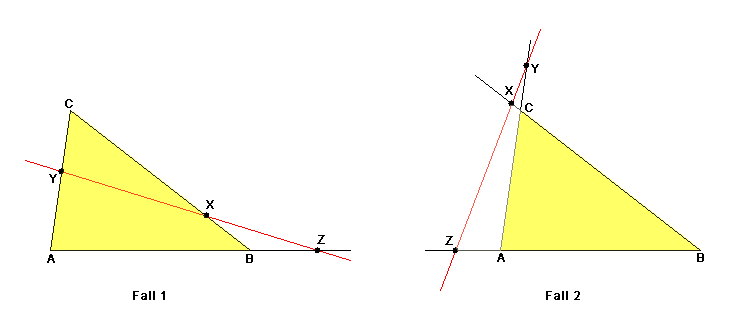
Gegeben seien ein Dreieck ABCABC und eine Gerade, welche die Dreiecksseiten BC‾\ovl{ BC}, CA‾\ovl{CA} und AB‾\ovl{AB} beziehungsweise ihre Verlängerungen in den Punkten XX, YY und ZZ schneidet. Dann gilt:
AZ‾⋅BX‾⋅CY‾=AY‾⋅BZ‾⋅CX‾\overline{AZ} \cdot \overline{BX} \cdot \overline{CY} = \overline{AY} \cdot \overline{BZ} \cdot \overline{CX}
Umgekehrt kann man aus der Richtigkeit dieser Beziehung folgern, dass die Punkte X, Y und Z auf einer Geraden liegen.
 
 

Beweis

Der Satz von Menelaos lässt sich mit Hilfe des Strahlensatzes beweisen. Man betrachtet drei Lote auf die gegebene Gerade, die von den Ecken A, B und C ausgehen. Die Längen der Lotstrecken seien mit a, ba,\, b und cc bezeichnet.
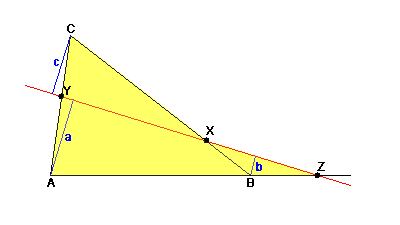
MenelaosBeweis.png
Aus dem Strahlensatz erhält man folgende Verhältnisgleichungen:
AZ‾:BZ‾=a:b\overline{AZ} : \overline{BZ} = a : b
BX‾:CX‾=b:c\overline{BX} : \overline{CX} = b : c
CY‾:AY‾=c:a\overline{CY} : \overline{AY} = c : a
Multipliziert man diese drei Gleichungen miteinander, so ergibt sich
AZ‾BZ‾⋅BX‾CX‾⋅CY‾AY‾=ab⋅bc⋅ca=a⋅b⋅cb⋅c⋅a=1\dfrac{\overline{AZ} }{\overline{BZ}} \cdot \dfrac{\overline{BX}}{\overline{CX}} \cdot \dfrac{\overline{CY}}{\overline{AY}} = \dfrac{a}{b} \cdot \dfrac{b}{c} \cdot \dfrac{c}{a} = \dfrac{a \cdot b \cdot c}{b \cdot c \cdot a} = 1
und weiter (durch Multiplikation mit dem Nenner)
AZ‾⋅BX‾⋅CY‾=AY‾⋅BZ‾⋅CX‾\overline{AZ} \cdot \overline{BX} \cdot \overline{CY} = \overline{AY} \cdot \overline{BZ} \cdot \overline{CX}.

Satz von Ceva

Der Satz von Ceva, benannt nach dem italienischen Mathematiker Giovanni Ceva (1647 bis 1734), macht eine Aussage über Dreieckstransversalen:
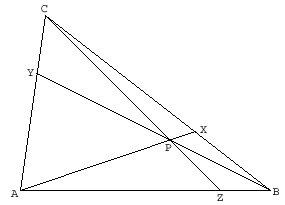
Ceva1.png
In einem Dreieck ABC seien [AX], [BY] und [CZ] drei Ecktransversalen (also Verbindungsstrecken zwischen einer Ecke und einem Punkt auf der gegenüber liegenden Seite beziehungsweise deren Verlängerung), die sich in einem Punkt P innerhalb oder außerhalb des Dreiecks schneiden. Dann gilt für die Längen der Seitenabschnitte:
AZ‾⋅BX‾⋅CY‾=AY‾⋅BZ‾⋅CX‾\overline{AZ} \cdot \overline{BX} \cdot \overline{CY} = \overline{AY} \cdot \overline{BZ} \cdot \overline{CX}
Diese Gleichung lässt sich mit Hilfe des Satzes von Menelaos beweisen.
Umgekehrt kann aus der Richtigkeit dieser Gleichung gefolgert werden, dass sich die Geraden AX, BY und CZ in einem Punkt schneiden.

Miß alles, was sich messen läßt, und mach alles meßbar, was sich nicht messen läßt.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Satz von Menelaos;wp:Satz von Ceva aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck