Satz von Stewart

Mit dem Satz von Stewart lässt sich die Länge einer Strecke durch die Ecke eines Dreiecks zur ihr gegenüberliegenden Seite berechnen.

Definition

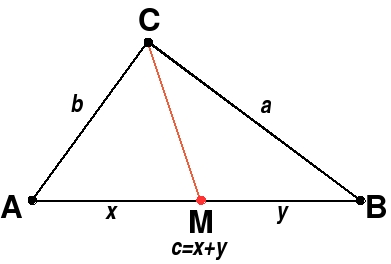
Satz_von_Stewart_Grafik.jpg
Konstruktion zum Satz von Stewart
Gegeben sei ein Dreieck (siehe Bild) mit den definierenden Eckpunkten A, B und C und den Seitenlängen
a=CB‾, b=AC‾a=\overline{CB},\, b=\overline{AC} und c=AB‾c=\overline{AB}.
Weiter sei M ein Punkt auf der Strecke AB‾\overline{AB} mit
x=AM‾, y=MB‾x=\overline{AM},\, y=\overline{MB} und c=x+y c=x+y \, .
Der Satz von Stewart besagt dann, dass
xa2+yb2=(x+y)CM‾2+xy2+yx2xa^2 + yb^2 = \braceNT{x+y}\overline{CM}^2 +xy^2+yx^2
Wird der Bruchteil AM‾\overline{AM} der Strecke AB‾\overline{AB} mit φ \phi \, bezeichnet dann gilt (mit φ′=1−φ\phi^\prime=1-\phi), dass
x=φc x=\phi c \, und y=φ′cy=\phi^\prime c
und der Satz lässt sich auch folgendermaßen formulieren:
CM‾2=a2φ+(c2φ−b2)φ′\overline{CM}^2=a^2 \phi + \braceNT{c^2\phi-b^2}\phi^\prime
 
 

Anwendungen

Der wichtige Satz des Heron zur Berechnung des Flächeninhalts eines Dreiecks aus seinen Seitenlängen folgt direkt aus dem Satz von Stewart.

Das Buch der Natur ist mit mathematischen Symbolen geschrieben.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Satz von Stewart aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck