Seitenhalbierende im Dreieck

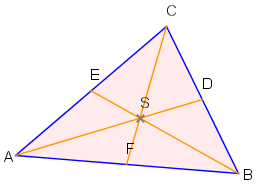
Seitenhalbierende.png
Die Seitenhalbierenden eines Dreiecks sind die Verbindungsstrecken zwischen jeweils einem Eckpunkt und dem Mittelpunkt der diesem gegenüberliegenden Seite.

Satz 5521A (Schnittpunkt der Seitenhalbierenden)

Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt, dem Schwerpunkt SS. Dieser teilt die Seitenhalbierenden im Verhältnis 2:1 vom Eckpunkt aus gesehen.

Beweis

Es gilt offensichtlich
CB‾CD‾=CA‾CE‾=21\dfrac{ \overline {CB} }{\overline {CD}}=\dfrac {\overline {CA} }{\overline {CE}}=\dfrac 2 1.
SeitenhalbierendeBew.png
Dann muss nach der Umkehrung der Strahlensätze AB‾∣∣ED‾\overline {AB}||\overline {ED} gelten, außerdem verhalten sie sich 2:12:1. Die Dreiecke △ESD\triangle ESD und △ABS\triangle ABS sind ähnlich (Übereinstimmung im Scheitelwinkel ∠ESD=∠BSA\angle ESD=\angle BSA und den Wechselwinkeln ∠SAB=∠SDE\angle SAB=\angle SDE). Dann gilt aber:
AS‾SD‾=BS‾SE‾=21\dfrac {\overline {AS}} {\overline {SD}}=\dfrac {\overline {BS} }{\overline {SE}}=\dfrac 2 1,
womit der erste Teil der Behauptung gezeigt ist.
Analoge Überlegungen kann man auch für zwei weitere Seitenhalbierende anstellen. Damit müssen sich dann aber alle drei Seitenhalbierenden in einem Punkt schneiden, denn es kann nur einen Punkt geben, der die Strecke BE‾\overline{BE} im Verhältnis 2:12:1 teilt.
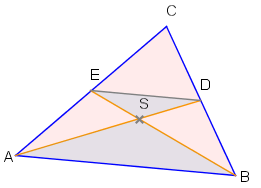
Um zu zeigen, dass SS der Schwerpunkt ist, zeigen wir, dass jede Seitenhalbierende das Dreieck in zwei flächengleiche Teildreiecke zerlegt, damit muss aber der Schnittpunkt zweier Seitenhalbierender der Schwerpunkt des Dreiecks sein.
SeitenhalbierendeBew2.png
Mit der Formel 5518B ergibt sich für deren Flächeninhalt A1A_1 des Dreiecks △ADC\triangle ADC
A1=12⋅a2⋅sa⋅sin⁡φA_1=\dfrac 1 2 \cdot\dfrac a 2\cdot s_a\cdot \sin\phi
und A2A_2 des Dreiecks △ABD\triangle ABD
A2=12⋅a2⋅sa⋅sin⁡(180°−φ)A_2=\dfrac 1 2 \cdot\dfrac a 2\cdot s_a\cdot \sin(180°-\phi)
Diese Ausdrücke sind aber wegen sin⁡φ=sin⁡(180°−φ)\sin\phi=\sin(180°-\phi) gleich. □\qed
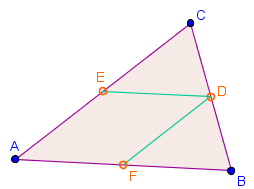
smpara.png

Satz A7RB

Die Seitenmittelpunkte bilden mit den einzelnen Eckpunkten ein Parallelogramm.

Beweis

Da Punkt DD die Seite BC‾\ovl{BC} halbiert und EE die Seite AC‾\ovl{AC} sind nach der Umkehrung der Strahlensätze die Strecken AB‾\ovl{AB} und ED‾\ovl{ED} parallel. Ebenso kann man AC‾∣∣DF‾\ovl{AC}|| \ovl{DF} schließen und das Viereck AFDEAFDE ist somit ein Parallelogramm. □\qed

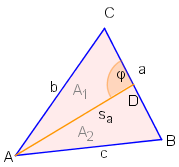
Formel 5522A (Länge der Seitenhalbierenden)

Für die Länge der Seitenhalbierenden sas_a der Seite aa gilt.
sa=122(b2+c2)−a2s_a=\dfrac 1 2\sqrt{2(b^2+c^2)-a^2}
Analoge Formeln lassen sich für die anderen Seitenhalbierenden aufstellen, indem man die Seiten zyklisch vertrauscht.

Herleitung

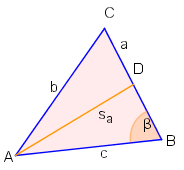
SeitenhalbierendeL.png
Mit dem Kosinussatz gilt im Dreieck △ABD\triangle ABD:
sa2=(a2)2+c2−2 a2 c⋅cos⁡βs_a^2={\braceNT{\dfrac a 2}}^2+c^2-2\, \dfrac a 2 \, c\cdot\cos\beta,(1)
und im Dreieck △ABC\triangle ABC gilt:
b2=a2+c2−2ac⋅cos⁡βb^2=a^2+c^2-2ac\cdot\cos\beta.(2)
Letztere Gleichung ist aber äquivalent zu
−2 a2 c⋅cos⁡β=b22−a22−c22-2\, \dfrac a 2 \, c\cdot\cos\beta=\dfrac {b^2} 2-\dfrac {a^2} 2-\dfrac {c^2} 2.(3)
Setzen wir diese Gleichung nun in (1) ein, erhalten wir
sa2=a24+c2+b22−a22−c22s_a^2={\dfrac {a^2} 4}+c^2+\dfrac {b^2} 2-\dfrac {a^2} 2-\dfrac {c^2} 2 =b22+c22−a24=\dfrac {b^2} 2+\dfrac {c^2} 2-\dfrac {a^2} 4 =14 (2(b2+c2)−a2)=\dfrac 1 4 \, \braceNT{2(b^2+c^2)-a^2},
woraus sich nach dem Wurzelziehen die Behauptung ergibt. □\qed
 
 

Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.

Karl Menger

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck