Satz über den Schwerpunkt im Dreieck

Der Schwerpunkt $G$ eines Dreiecks $\triangle ABC$ teilt die Verbindungsstrecke von Umkreismittelpunkt $O$ und Höhenschnittpunkt $P$ im Verhältnis $1:2$.

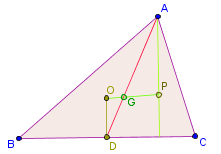
Die Dreiecke $\triangle GAP$ und $\triangle GDO$ sind ähnlich (sie stimmen im Scheitelwinkel im Punkt $G$ und den Wechselwinkeln in den Punkten $A$ und $D$ überein). Nach Satz 5515G gilt $|\ovl {AP}|=2\cdot |\ovl {OD}|$, also wegen der Ähnlichkeit auch $|\ovl {GP}|=2\cdot |\ovl {GO}|$. $\qed$
Aus dieser Ähnlichkeit erhalten wir außerdem noch die Behauptung von Satz 5521A, dass der Schwerpunkt die Seitenhalbierenden im Verhältnis $1:2$ teilt, denn es gilt auch $|\ovl {GA}|=2\cdot |\ovl {GD}|$.