Peripheriewinkelsatz
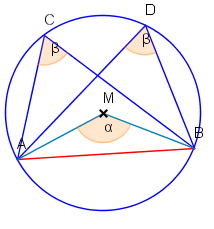
Bei der Definition des Peripheriewinkels haben wir diese in der nebenstehenden Abbildung etwas lax beide mit bezeichnet ohne uns groß Gedanken darum zu machen, ob sie wirklich gleichgroß sind. Dies ist aber genau die Aussage des Peripheriewinkelsatzes.
Satz 5513B (Peripheriwinkelsatz/ Umfangswinkelsatz)
Alle Peripheriwinkel (in der gleichen Halbebene) über dem gleichen Kreisbogen sind gleichgroß
Beweis
Unter Zuhilfenahme des Zentri-Peripherie-Winkelsatzes ergibt sich die Behauptung sofort. Denn die Winkel und sind beide Peripheriwinkel zum gleichen Zentriwinkel . Sind also beide halb so groß wie und damit untereinander gleich.
Den Peripheriewinkelsatz kann man auch umkehren und damit zur Charakterisierung eines Kreises verwenden.
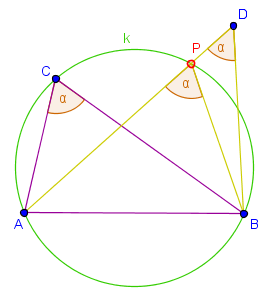
Satz A7RC (Umkehrung des Peripheriewinkelsatzes)
Über einer Strecke werden die Punkte und so gewählt, dass sie in einer Halbebene liegen und . Dann liegen die Punkte , , und auf einem Kreis.
Beweis
Wir bilden den Kreis um die Punkte , und . Angenommen liegt nicht auf diesem Kreis. Dann gibt es einen Punkt , der auf der Geraden durch und liegt und den Kreis schneidet. Nach dem Peripheriewinkelsatz ist nun aber . Die Dreiecke und sind kongruent, da sie in einer Seite und 3 Winkeln übereinstimmen und müssen sogar identisch übereinander liegen, da sie zwei gemeinsame Punkte haben. Damit müssen aber die Punkte und übereinstimmen, im Widerspruch zur Annahme, dass nicht auf dem Kreis liegt.
Um Peripheriewinkel zu berechnen kann man sich folgende Beziehung zu Nutze machen:
Formel 5513C
,
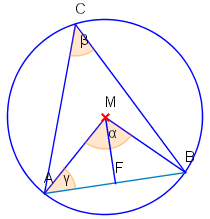
Beweis
Sei der Peripheriwinkel und der zugehörige Zentriwinkel. Nach dem Zentri-Peripheri-Winkelsatz gilt: .
Der Punkt ist der Lotfußpunkt von auf . Wegen der Gleichschenkligkeit des Dreiecks halbiert das Lot den Winkel .
Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.
Leonardo da Vinci
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе