Flächeninhalt und Umfang des Kreises

Für die Berechnung von Flächeninhalt und Umfang spielt die Kreiszahl $\pi\approx 3,1415926$ eine besondere Rolle. Sie ist definiert als das Verhältnis von Umfang und Durchmesser des Kreises.

Für den Umfang $u$ ergibt sich damit:

Auch beim Flächeninhalt $A$ findet man diese Zahl wieder:

Unter allen geschlossenen ebenen Figuren gleichen Umfangs besitzt der Kreis den größten Flächeninhalt.

Zuerst zeigen wir, dass die flächengrößte Figur konvex sein muss. Nehmen wir an, sie wäre nicht konvex. Wir bilden dann die konvexe Hülle und spiegeln alle Gebiete, die innerhalb der Hülle aber nicht in der Figur selbst liegen am Rand der konvexen Hülle. Die so entstehende Figur hat den gleichen Umfang wie die Ausgangsfigur aber einen größeren Flächeninhalt. Damit ist die gesuchte Figur konvex.

Wir finden jetzt zwei Randpunkte, die den Umfang in zwei gleiche Teile teilen, und deren Verbindungsstrecke in der Figur liegt. Diese Stecke halbiert auch den Flächeninhalt der Figur. Denn andernfalls würden wir die größere Hälfte nehmen, an der Strecke spiegeln und hätten eine Figur mit gleichem Umfang aber größerem Flächeninhalt.

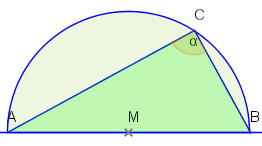
Wir zeigen, dass die Hälften Halbkreise sind. Wenn die Hälfte kein Halbkreis ist, dann finden wir einen Punkt $C$ auf der Kurve so dass für den Winkel $\alpha\neq 90°$ gilt. Unter Beibehaltung der Bogenlänge und Flächengröße der Kreissektoren über $\overline{AC}$ und $\overline{AB}$ verschieben wir den Punkt $C$ solange, bis der Winkel $\alpha=90°$ ist. Die Fläche des Dreiecks $\triangle ABC$ ist dann maximal und somit auch die Fläche der Halbfigur. Diese muss nach dem Satz des Thales aber ein Halbkreis sein. $\qed$