Kreisabschnitt

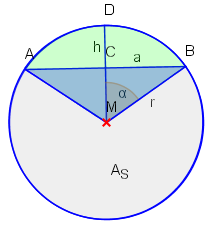
KAbschnitt.png
Durch die Sehne AB‾\overline{AB} wird der Kreis in zwei Abschnitte eingeteilt.
Wir definieren die Größen rr für den Radius des Kreises, h=∣CD‾∣h=|\overline{CD}| und a=∣CB‾∣=∣AB‾∣/2a=|\overline{CB}|=|\overline{AB}|/2, sowie α=∠BMC\alpha=\angle BMC.
Um den Flächeninhalt AA des durch A,BA,B und DD bestimmten Sektors zu berechnen benutzen wir den Ansatz
A=AK−AD−ASA=A_K-A_D-A_S,(1)
dabei sind AK=πr2A_K=\pi r^2 der Inhalt des Kreises, ADA_D der Flächeninhalt des Dreiecks △AMB\triangle AMB, und ASA_S der Inhalt des Kreissektors ABMABM (hellgrau in der Grafik).
Es gilt
AS=(π−α)r2A_S=(\pi-\alpha)r^2(2)
und nach Formel 5504A
AD=2⋅12a(r−h)=a(r−h)A_D=2\cdot \dfrac 1 2 a(r-h)=a(r-h).(3)
Zusammen mit (1) ergibt sich:
A=πr2−(π−α)r2−a(r−h)=αr2−a(r−h)A=\pi r^2-(\pi-\alpha)r^2-a(r-h)=\alpha r^2-a(r-h).(4)
Für die Bestimmung von α\alpha benutzen wir die Definition des Kosinus
cos⁡α=r−hr=1−hr\cos\alpha=\dfrac {r-h} r=1-\dfrac h r,(5)
und für aa hilft der Satz des Pythagoras weiter:
a2+(r−h)2=r2a^2+(r-h)^2=r^2,(6)
was nach aa umgestellt
a=h(2r−h)a=\sqrt{h(2r-h)}(7)
ergibt.
Setzt man (5) und (7) in (4) ein, erhält man eine Flächenformel, die nur von rr und hh abhängt:

Formel 5509A (Flächeninhalt des Kreisabschnitts)

A=arccos⁡(1−hr) r2−h(2r−h)(r−h)A=\arccos\braceNT{1-\dfrac h r}\, r^2-\sqrt{h(2r-h)}(r-h)
 
 

Man darf nicht das, was uns unwahrscheinlich und unnatürlich erscheint, mit dem verwechseln, was absolut unmöglich ist.

Carl Friedrich Gauß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie