Die Kreiszahl Pi

Die Kreiszahl π\pi (sprich Pi) ist eine reelle Zahl und mathematische Konstante. Ihr Wert beträgt näherungsweise
π ≈ 3,1415926\pi \, \approx \, 3,1415926.
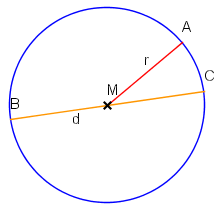
320_Kreis.png
Kreis mit eingezeichnetem Mittelpunkt (M), Radius (r) und Durchmesser (d)

Definition und Eigenschaften

Gemeinhin definiert man π\pi als das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Dieser Wert ist für alle Kreise konstant. Eine weitere Möglichkeit besteht darin, die Kreiszahl als Größe der Fläche eines Kreises mit dem Radius 11 zu definieren.
 
 

Irrationalität und Transzendenz

Die Zahl π\pi ist keine rationale Zahl, sie lässt sich also nicht als Bruch darstellen. Sie ist sogar eine sogenannte transzendente Zahl, d.h. es gibt kein Polynom mit rationalen Koeffizienten, deren Nullstelle π\pi ist. Dies liefert auch die Begründung dafür, dass das aus der Antike überlieferte Problem der Quadratur des Kreises nicht lösbar ist.

Vorkommen und Anwendungen

Die Zahl π\pi findet sich in vielen Formeln der Mathematik, Physik und Naturwissenschaft. Immer wenn ein Kreis, oder etwas Periodisches ein Rolle spielt findet man Pi in den entsprechenden Formeln. Darüber hinaus findet man die Kreiszahl auch in Formeln, wo man ihr Auftreten nicht vermuten würde.
n!≈2πn(ne)nn! \approx \sqrt{2 \pi n} \braceNT{\dfrac{n}{e}}^n (Stirling-Formel als Näherung der Fakultät für große nn) eiπ+1=0e^{i \pi} +1 = 0 (Eulersche Formel)

Darstellungen der Zahl Pi

Unendliche Reihen

∑n=0∞(−1)n2n+1=1−13+15−⋯=π4 \sum\limits_{n=0}^{\infty} \dfrac{(-1)^n}{2n+1} = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dots = \dfrac{\pi}{4} Leibniz
112+122+132+142+⋯=π26\dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2} + \dots = \dfrac{\pi^2}{6} Euler
112+132+152+172+192+⋯=π28\dfrac1{1^2}+\dfrac1{3^2}+\dfrac1{5^2}+\dfrac1{7^2}+\dfrac1{9^2}+\cdots= \dfrac{\pi^2}8
12⋅3⋅4−14⋅5⋅6+16⋅7⋅8−+⋯=π−34\dfrac{1}{2\cdot3\cdot4} - \dfrac{1}{4\cdot5\cdot6} + \dfrac{1}{6\cdot7\cdot8} - + \dots = \dfrac{\pi - 3}{4}
∑k=0∞116k(48k+1−28k+4−18k+5−18k+6)=π \sum\limits_{k=0}^{\infty}\dfrac{1}{16^k}\braceNT{\dfrac{4}{8k+1} - \dfrac{2}{8k+4} - \dfrac{1}{8k+5} - \dfrac{1}{8k+6}} =\pi Bailey-Borwein-Plouffe-Formel/ BBP-Reihe

Unendliche Produkte

21⋅23⋅43⋅45⋅65⋅67⋅87⋅89⋅⋯=π2 \dfrac{2}{1} \cdot \dfrac{2}{3} \cdot \dfrac{4}{3} \cdot \dfrac{4}{5} \cdot \dfrac{6}{5} \cdot \dfrac{6}{7} \cdot \dfrac{8}{7} \cdot \dfrac{8}{9} \cdot \dots = \dfrac{\pi}{2} Wallissches Produkt
22⋅2+22⋅2+2+22⋅⋯=2π\dfrac{\sqrt2}2 \cdot \dfrac{\sqrt{2+\sqrt2}}2 \cdot \dfrac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \dots = \dfrac2{\pi}

Kettenbrüche

4π=1+123+225+327+429+5211+62⋯\dfrac{4}{\pi}=1+\dfrac{1^2}{3+\dfrac{2^2}{5+\dfrac{3^2}{7+\dfrac{4^2}{9+\dfrac{5^2}{11+\dfrac{6^2}{\cdots}}}}}} Johann Heinrich Lambert
π=41+122+322+522+722+⋯\pi = \dfrac{4}{1 + \dfrac{1^2}{2 + \dfrac{3^2}{2 + \dfrac{5^2}{2 + \dfrac{7^2}{2 + \cdots}}}}}

An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie