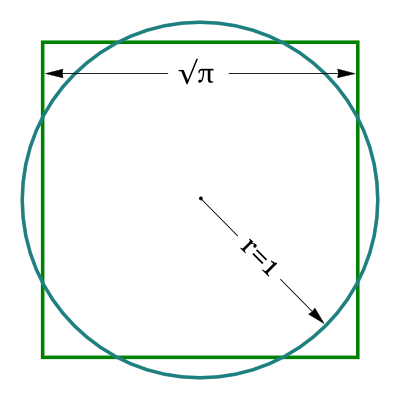
Quadratur des Kreises

Squaring_the_circle.png
Das Quadrat und der Kreis haben den gleichen Flächeninhalt.
Bei der Quadratur des Kreises soll aus einem gegebenen Kreis in endlich vielen Schritten ein Quadrat mit demselben Flächeninhalt konstruiert werden. Beschränkt man die Konstruktionsmittel auf Zirkel und Lineal, ist die Aufgabe unlösbar.
Die Quadratur des Kreises gehörte jahunderte lang zu den populärsten ungelösten Problemen der Mathematik. Der Begriff Quadratur des Kreises ist in vielen Sprachen zu einer Metapher für eine unlösbare Aufgabe geworden. Die Unlösbarkeit konnte jedoch erst im Jahr 1882 bewiesen werden.

Algebraische Problemstellung

Zur Lösung des Problems bedurfte es zum einen der Möglichkeit, dem geometrischen Begriff "konstruierbar" eine algebraische Bedeutung zu geben, zum anderen genauerer Einsicht der Eigenschaften der Kreiszahl.
Eine geometrische Konstruktion mit Zirkel und Lineal geht von einer endlichen Anzahl vorgegebener Punkte aus und ermittelt in einer endlichen Anzahl von Schritten neue Punkte durch das Schneiden zweier Geraden, zweier Kreise oder einer Geraden mit einem Kreis. Geraden und Kreise werden durch Gleichungen beschrieben, Schnittpunkte werden durch das Lösen von Gleichungssystemen bestimmt. Es stellt sich heraus, dass die mit Zirkel und Lineal konstruierbaren Streckenlängen genau die sind, die sich durch eine endliche Zahl von rationalen Operationen (Addition, Subtraktion, Multiplikation und Division) sowie einer endlichen Anzahl von Quadratwurzeln aus einer vorgegebenen Länge ableiten lassen. Insbesondere sind diese Längen algebraische Zahlen, also eine Teilmenge der Zahlen, die eine Lösung einer algebraischen Gleichung beliebigen Grades mit rationalen Koeffizienten sind. Zahlen, die nicht algebraisch sind, heißen transzendent und sind nicht konstruierbar.

Beweis der Unmöglichkeit

Ferdinand von Lindemann konnte 1882 beweisen, dass π\pi transzendent ist und deshalb die Quadratur des Kreises unmöglich ist.
Ausgehend von der Tranzendenz der eulerschen Zahl ee bewies er, dass für beliebige voneinander verschiedene algebraische Zahlen z1,…,zrz_1 , \dots , z_r und für beliebige algebraische Zahlen n1,…,nrn_1 , \dots , n_r die Gleichung
∑i=1rniezi=0\sum\limits_{i=1}^{r} n_i e^{z_i} = 0
nur dann gelten kann, wenn alle nin_i den Wert Null haben. Insbesondere kann für keine von Null verschiedene algebraische Zahl zz der Ausdruck eze^z eine rationale Zahl ergeben. Nach dieser Vorbereitung konnte Lindemann die Annahme, π\pi sei algebraisch, mithilfe der Eulerschen Identität eiπ=−1e^{i\pi} = -1 zum Widerspruch führen; π\pi musste somit transzendent sein.

Näherungskonstruktionen

Obwohl eine exakte Lösung mit Zirkel und Lineal nicht möglich ist, gibt es Näherungskonstruktionen für die Kreisquadratur. Einfache, schon in der Antike bekannte Verfahren geben ein ganzzahliges Verhältnis von Durchmesser oder Radius des Kreises zur Seite oder Diagonalen des Quadrates an.
Eine klassische Näherungslösung ist die Näherungskonstruktion von Kochański. Sie kommt mit nur einer Zirkelöffnung aus. Die eigentliche Konstruktion besteht aus einer Rektifikation des Halbkreises, Kochanski konstruierte aus dem vorgegebenen Radius rr näherungsweise eine gerade Strecke der Länge rπr \pi. Die Quadratur folgt daraus elementar mithilfe des Kathetensatzes. Die Kreiszahl wird bei Kochański auf vier Nachkommastellen genau angenähert:
π≈403−23=3,141533…\pi \approx \sqrt{\dfrac{40}{3}-2\sqrt{3}} = 3{,}141533\dots
Im Jahr 1913 erschien eine Konstruktion des indischen Mathematikers S. A. Ramanujan,die auf der Näherung
π≈355113=3,1415929…\pi\approx\dfrac{355}{113} = 3{,}1415929\dots
beruht. In einer Arbeit aus dem Folgejahr lieferte Ramanujan neben anderen Näherungsverfahren eine weitere Quadratur mit Zirkel und Lineal. Dieser liegt der Wert
π≈92+192224=3,141592652…\pi\approx\sqrtN{4}{9^2 + \dfrac{19^2}{22}} = 3{,}141592652\dots
zugrunde, der π\pi sogar auf acht Stellen nahe kommt.
Eine einfachere Methode veröffentlichte Louis Loynes 1961.Sie beruht auf der Feststellung, dass der Flächeninhalt des Umkreises eines rechtwinkligen Dreiecks gleich dem Quadrat über der größeren Kathete ist, wenn der Tangens des kleineren Winkels, also das Verhältnis von kleinerer zu größerer Kathete,
4π−1=0,5227232… \sqrt{\dfrac{4}{\pi}-1} = 0{,}5227232\dots
beträgt, ein Wert, der sehr nahe an dem Bruch
2344=0,5227272… \dfrac{23}{44} = 0{,}5227272\dots
liegt. Daraus ergibt sich eine einfache Näherung, indem man das (konstruierbare) rechtwinklige Dreieck mit dem Katheten-Verhältnis 23:44 zur Quadratur benutzt. Der angenäherte Wert für die Kreiszahl von
π≈77442465=3,141582…\pi\approx\dfrac{7744}{2465} = 3{,}141582\dots
ist etwas besser als bei Kochańskis Konstruktion.
 
 

Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Quadratur des Kreises aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Grundbegriffe