Tangens und Kotangens
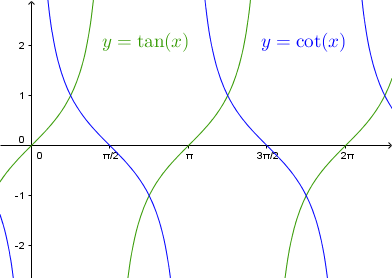
Abb. 1: Graphen der Tangens- und
Kotangensfunktion (Argument
x x x im
Bogenmaß ).
Geometrische Definition
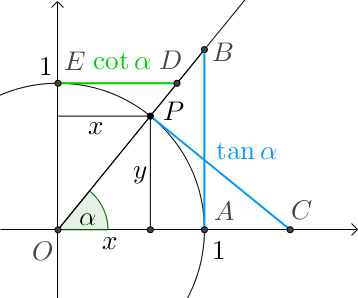
Abb. 2:
Tangens am Einheitskreis: Die Länge der blauen
Strecken entspricht dem
Tangens und die der grünen
Strecke dem
Kotangens .
Sei
P \displaystyle{{P}} P ein
Punkt auf dem Einheitskreis, der mit der
x \displaystyle{{x}} x -Achse den
Winkel α \displaystyle{\alpha} α einschließt (vgl. Abb. 2). Dann sind
Tangens und
Kotangens wie folgt definiert:
tan α = y x \tan \alpha=\frac y x tan α = x y cot α = x y \cot \alpha=\frac x y cot α = y x Mittels
Strahlensatz ergibt sich
tan α = y x = A B ‾ 1 \displaystyle{{\tan{\alpha}}=\frac{{y}}{{x}}=\frac{\overline{{{A}{B}}}}{{1}}} tan α = x y = 1 A B . Damit entspricht die Länge der
Strecke A B ‾ \displaystyle{\overline{{{A}{B}}}} A B dem
Tangens des
Winkels α \displaystyle{\alpha} α .
Die
Tangente an den Einheitskreis im
Punkt P \displaystyle{{P}} P schneide die
x \displaystyle{{x}} x -Achse im
Punkt C \displaystyle{{C}} C . Die
Dreiecke △ O A B \displaystyle{\triangle{O}{A}{B}} △ O A B und
△ O C P \displaystyle{\triangle{O}{C}{P}} △ O C P sind kongruent, denn sie stimmen in zwei
Winkeln (
α \displaystyle{\alpha} α und dem
rechten Winkel bei
A A A bzw. bei
P P P ) und der Seite
∣ O P ‾ ∣ = ∣ O A ‾ ∣ = 1 \displaystyle{{\left|\overline{{{O}{P}}}\right|}={\left|\overline{{{O}{A}}}\right|}={1}} ∣ ∣ O P ∣ ∣ = ∣ ∣ O A ∣ ∣ = 1 überein. Daher gilt:
tan α = ∣ A B ‾ ∣ = ∣ P C ‾ ∣ \displaystyle{{\tan{\alpha}}={\left|\overline{{{A}{B}}}\right|}={\left|\overline{{{P}{C}}}\right|}} tan α = ∣ ∣ A B ∣ ∣ = ∣ ∣ P C ∣ ∣
Der Tangens entspricht also der Länge des Tangentenabschnitts, woher sich der Name Tangens ableitet.
Analog gilt
cot α = x y = ∣ E D ‾ ∣ 1 \displaystyle{{\cot{\alpha}}=\frac{{x}}{{y}}=\frac{{{\left|\overline{{{E}{D}}}\right|}}}{{1}}} cot α = y x = 1 ∣ ∣ E D ∣ ∣ , womit die Länge der
Strecke E D ‾ \displaystyle{\overline{{{E}{D}}}} E D dem
Kotangens entspricht.
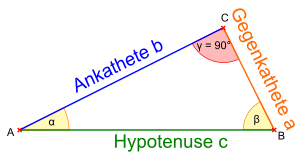
In einem
rechtwinkligen Dreieck ist der
Tangens eines
Winkels α \alpha α das Längenverhältnis von Gegenkathete zu Ankathete und der
Kotangens das Längenverhältnis von Ankathete zu Gegenkathete:
tan α = l Gegenkathete l Ankathete = a b = sin α cos α \tan \alpha =\dfrac{l_\text{Gegenkathete}}{l_\text{Ankathete}}=\dfrac{a}{b} = \dfrac{\sin \alpha}{\cos \alpha} tan α = l Ankathete l Gegenkathete = b a = cos α sin α cot α = l Ankathete l Gegenkathete = b a = cos α sin α \cot \alpha=\dfrac{l_\text{Ankathete}}{l_\text{Gegenkathete}} = \dfrac{b}{a} = \dfrac{\cos \alpha}{\sin \alpha} cot α = l Gegenkathete l Ankathete = a b = sin α cos α Satz 5220C (Eingenschaften von Tangens und Kotangens)
tan α ⋅ cot α = 1 cot α = 1 tan α \tan \alpha\cdot\cot \alpha=1 \qquad\qquad \cot \alpha =\dfrac 1 {\tan \alpha} tan α ⋅ cot α = 1 cot α = tan α 1 tan ( π 2 − α ) = cot α cot ( π 2 − α ) = tan α \tan \braceNT{\dfrac \pi 2-\alpha}=\cot \alpha\qquad \cot \braceNT{\dfrac \pi 2-\alpha}=\tan \alpha tan ( 2 π − α ) = cot α cot ( 2 π − α ) = tan α tan α = sin α cos α \displaystyle{{\tan{\alpha}}=\frac{{{\sin{\alpha}}}}{{{\cos{\alpha}}}}} tan α = cos α sin α \qquad\qquad cot α = cos α sin α \displaystyle{{\cot{\alpha}}=\frac{{{\cos{\alpha}}}}{{{\sin{\alpha}}}}} cot α = sin α cos α
Tangens und Kotangens sind ungerade Funktionen : tan ( − x ) = − tan x cot ( − x ) = − cot x \tan(-x) = -\tan x \qquad\qquad \cot(-x) = -\cot x tan ( − x ) = − tan x cot ( − x ) = − cot x
Beweis
(i) und (iv) folgen direkt aus den Definitionen.
(ii) Mit
Satz 5220B :
tan ( π 2 − α ) = sin ( π 2 − α ) cos ( π 2 − α ) \tan \braceNT{\dfrac \pi 2-\alpha}=\dfrac {\sin \braceNT{\dfrac \pi 2-\alpha}}{\cos \braceNT{\dfrac \pi 2-\alpha}} tan ( 2 π − α ) = cos ( 2 π − α ) sin ( 2 π − α ) = cos α sin α = cot α =\dfrac{\cos \alpha}{\sin \alpha}=\cot \alpha = sin α cos α = cot α .
Kotangens analog.
□ \qed □ Weitere Eigenschaften
Periodizität
Periodenlänge
π \pi π (halbe
Drehung ):
tan ( x + π ) = tan ( x ) \tan(x+\pi) = \tan(x) tan ( x + π ) = tan ( x ) Monotonie
Nullstellen
Tangens: x = n ⋅ π ; n ∈ Z x = n \cdot \pi\, ;\quad n \in \mathbb{Z} x = n ⋅ π ; n ∈ Z Kotangens: x = ( 1 2 + n ) ⋅ π ; n ∈ Z x = \left(\frac{1}{2} + n\right) \cdot \pi\, ;\quad n \in \mathbb{Z} x = ( 2 1 + n ) ⋅ π ; n ∈ Z Polstellen
Tangens: x = ( 1 2 + n ) ⋅ π ; n ∈ Z x = \left(\frac{1}{2} + n\right) \cdot \pi\, ;\quad n \in \mathbb{Z} x = ( 2 1 + n ) ⋅ π ; n ∈ Z Kotangens: x = n ⋅ π ; n ∈ Z x = n \cdot \pi\, ;\quad n \in \mathbb{Z} x = n ⋅ π ; n ∈ Z Wendestellen
Tangens: x = n ⋅ π ; n ∈ Z x = n \cdot \pi\, ;\quad n \in \mathbb{Z} x = n ⋅ π ; n ∈ Z Kotangens: x = ( 1 2 + n ) ⋅ π ; n ∈ Z x = \left(\frac{1}{2} + n\right) \cdot \pi\, ;\quad n \in \mathbb{Z} x = ( 2 1 + n ) ⋅ π ; n ∈ Z Sowohl die
Tangensfunktion als auch die
Kotangensfunktion haben
Asymptoten , aber keine Sprungstellen oder Extrema.
Spezielle Funktionswerte
Tangens
Kotangens
Wert
num. Wert
tan 0 ∘ \tan0^\circ tan 0 ∘
cot 9 0 ∘ \cot90^\circ cot 9 0 ∘
0 0 0
0
tan 1 5 ∘ \tan15^\circ tan 1 5 ∘
cot 7 5 ∘ \cot75^\circ cot 7 5 ∘
2 − 3 2 - \sqrt3 2 − 3
0.2679491…
tan 22 , 5 ∘ \tan22{,}5^\circ tan 2 2 , 5 ∘
cot 67 , 5 ∘ \cot67{,}5^\circ cot 6 7 , 5 ∘
2 − 1 \sqrt2-1 2 − 1
0,4142135…
tan 3 0 ∘ \tan30^\circ tan 3 0 ∘
cot 6 0 ∘ \cot60^\circ cot 6 0 ∘
1 / 3 1/\sqrt3 1 / 3
0,5773502…
tan 4 5 ∘ \tan45^\circ tan 4 5 ∘
cot 4 5 ∘ \cot45^\circ cot 4 5 ∘
1 1 1
1
tan 6 0 ∘ \tan60^\circ tan 6 0 ∘
cot 3 0 ∘ \cot30^\circ cot 3 0 ∘
3 \sqrt3 3
1,7320508…
tan 67 , 5 ∘ \tan67{,}5^\circ tan 6 7 , 5 ∘
cot 22 , 5 ∘ \cot22{,}5^\circ cot 2 2 , 5 ∘
2 + 1 \sqrt2+1 2 + 1
2,4142135…
tan 7 5 ∘ \tan75^\circ tan 7 5 ∘
cot 1 5 ∘ \cot15^\circ cot 1 5 ∘
2 + 3 2 + \sqrt3 2 + 3
3.7320508…
Reihenentwicklung
Tangens
Die
Taylorreihe mit dem Entwicklungspunkt
x = 0 x = 0 x = 0 (Maclaurinsche Reihe) lautet für
∣ x ∣ < π 2 |x|<\frac{\pi}{2} ∣ x ∣ < 2 π tan x = x + 1 3 x 3 + 2 15 x 5 + 17 315 x 7 + ⋯ = ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ 2 2 n ⋅ ( 2 2 n − 1 ) ⋅ B 2 n ( 2 n ) ! x 2 n − 1 . \begin{array}{cl} \tan x &= x+\frac13 x^3+\frac{2}{15}x^5+\frac{17}{315}x^7+\dotsb\\ &= \sum_{n=1}^\infty \frac{(-1)^{n-1} \cdot 2^{2n} \cdot \left(2^{2n} -1\right) \cdot B_{2n}}{(2n)!} x^{2n - 1}. \end{array} tan x = x + 3 1 x 3 + 1 5 2 x 5 + 3 1 5 1 7 x 7 + ⋯ = ∑ n = 1 ∞ ( 2 n ) ! ( − 1 ) n − 1 ⋅ 2 2 n ⋅ ( 2 2 n − 1 ) ⋅ B 2 n x 2 n − 1 . Kotangens
Die Laurent-Reihe lautet für
0 < ∣ x ∣ < π 0<|x|<\pi 0 < ∣ x ∣ < π cot x = 1 x − 1 3 x − 1 45 x 3 − 2 945 x 5 − 1 4725 x 7 − ⋯ = ∑ n = 0 ∞ ( − 1 ) n 2 2 n B 2 n ( 2 n ) ! x 2 n − 1 . \begin{array}{cl} \cot x &= \frac 1x - \frac 13x - \frac 1{45}x^3 - \frac 2{945}x^5 - \frac 1{4725}x^7 - \dotsb\\ &=\sum_{n=0}^\infty (-1)^n\frac{2^{2n} B_{2n}}{(2n)!} x^{2n - 1}. \end{array} cot x = x 1 − 3 1 x − 4 5 1 x 3 − 9 4 5 2 x 5 − 4 7 2 5 1 x 7 − ⋯ = ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! 2 2 n B 2 n x 2 n − 1 . π cot π x = 1 x + ∑ k = 1 ∞ ( 1 x + k + 1 x − k ) = 1 x + ∑ k = 1 ∞ 2 x x 2 − k 2 . \begin{array}{cl} \pi\cot\pi x &= \frac1x+\sum_{k=1}^\infty\left(\frac1{x+k}+\frac1{x-k}\right)\\ &= \frac1x+\sum_{k=1}^\infty\frac{2x}{x^2-k^2}. \end{array} π cot π x = x 1 + ∑ k = 1 ∞ ( x + k 1 + x − k 1 ) = x 1 + ∑ k = 1 ∞ x 2 − k 2 2 x . Ableitung
d d x tan x = 1 + tan 2 x = 1 cos 2 x = sec 2 x \frac{\mathrm d}{\mathrm dx}\tan x = 1 + \tan^2 x = \frac{1}{\cos^2 x}=\sec^2 x d x d tan x = 1 + tan 2 x = cos 2 x 1 = sec 2 x d d x cot x = − 1 − cot 2 x = − 1 sin 2 x = − csc 2 x \frac{\mathrm d}{\mathrm dx}\cot x = -1 - \cot^2 x = -\frac1{\sin^2x}=- \csc^2 x d x d cot x = − 1 − cot 2 x = − sin 2 x 1 = − csc 2 x Stammfunktionen
Tangens :
∫ tan ( a x + b ) d x = − ln ∣ cos ( a x + b ) ∣ a + C \int \tan (ax+b)\ \mathrm dx = - \frac{\ln|\cos (ax+b)|}{a}+C ∫ tan ( a x + b ) d x = − a ln ∣ cos ( a x + b ) ∣ + C a x + b ≠ ( 2 k + 1 ) π 2 ( k ∈ Z ) ax + b \ne (2k +1)\frac{\pi}{2} (k \in \mathbb{Z}) a x + b = / ( 2 k + 1 ) 2 π ( k ∈ Z ) Kotangens :
∫ cot ( a x + b ) d x = ln ∣ sin ( a x + b ) ∣ a + C \int \cot (ax+b)\ \mathrm dx = \frac{\ln|\sin (ax+b)|}{a}+C ∫ cot ( a x + b ) d x = a ln ∣ sin ( a x + b ) ∣ + C a x + b ≠ k π ( k ∈ Z ) ax + b \ne k\pi (k \in \mathbb{Z}) a x + b = / k π ( k ∈ Z ) Es gibt Dinge, die den meisten Menschen unglaublich erscheinen, die nicht Mathematik studiert haben.
Archimedes
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе