Logarithmusfunktionen

Die Logarithmusfunktion ist die Umkehrung der Exponentialfunktion. Im Fall, das die [!Basis] die Eulersche Zahl e⁡\e ist, heißt die Umkehrung von e⁡x\e^x natürlicher Logarithmus und wird mit ln⁡(x)\ln(x) bezeichnet. Die Umkehrung der allgemeinen Exponentialfunktion axa^x (a>0a>0, a≠1a\neq 1) ist dementsprechend y=log⁡axy=\log_a x. Im Fall von a=10a=10 spricht man vom dekadischen Logarithmus und schreibt auch log⁡x\log x; falls a=2a=2 heißt er binärer Logarithmus und wird mit lb(x)\mathbb{lb}(x) bezeichnet.
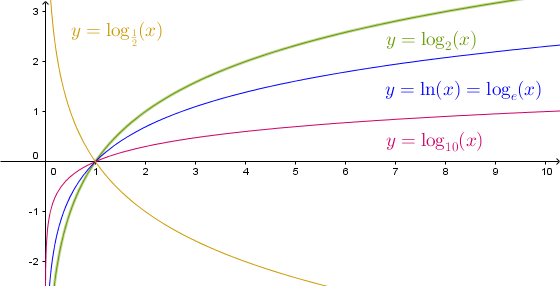
log.png
Die Graphen dreier Logarithmusfunktionen zur [!Basis] 12\frac 1 2, 22, e⁡\e und 1010.

Eigenschaften

Die Logarithmusfunktionen sind streng monoton wachsend (für a>1a>1) und streng monoton fallend (für a<1a<1). Sie besitzen daher keine Extrema und keine Wendepunkte.
Sie haben eine Nullstelle bei x0=1x_0=1. Ihr Definitionsbereich sind die positiven reellen Zahlen R+\R^+ und ihr Wertebereich alle reellen Zahlen, also log⁡a:R+→R\log_a: \R^+\to \R.

Asymptotisches Verhalten

lim⁡x→+0log⁡ax={−∞,fu¨r a>1+∞,fu¨r a<1 \lim_{x \to +0} \log_a x = \begin{cases} -\infty, & \text{für } a\gt 1\\ +\infty, & \text{für } a<1 \end{cases}
lim⁡x→∞log⁡ax={+∞,fu¨r a>1−∞,fu¨r b<1\lim_{x \to \infty} \log_a x = \begin{cases} +\infty, & \text{für } a\gt 1\\ -\infty, & \text{für } b<1 \end{cases}

Reihenentwicklungen

Der natürliche Logarithmus kann als Potenzreihe
ln⁡(1+x)=∑k=1∞(−1)k+1xkk\ln(1+x) = \sum_{k=1}^\infty (-1)^{k+1} \frac{x^k}k =x−x22+x33−x44+⋯= x-\frac{x^2}2 + \frac{x^3}3 -\frac{x^4}4 + \dotsb
darstellen, die im halboffenen Intervall ]−1,1]]-1,1] konvergiert. Zur Berechnung des Werts von ln⁡(1+x)\ln(1+x) für x>1x>1 verwendet man ln⁡(1+x)=−ln⁡(1+(−x1+x))\ln(1+x)=-\ln\Bigl(1+\Bigl(-\frac x{1+x}\Bigr)\Bigr).
Auf der Potenzreihenentwicklung des Areatangens Hyperbolicus beruht die folgende Reihenentwicklung, die für alle x>0x>0 konvergiert:
ln⁡x=∑k=0∞22k+1⋅(x−1x+1)2k+1 \ln x = \sum_{k=0}^{\infty} \frac{2}{2k+1} \cdot \left(\frac{x-1}{x+1}\right)^{2k+1} .
Diese Reihe konvergiert umso besser, je näher xx bei 11 liegt.

Funktionalgleichung

Die Logarithmusfunktionen genügen der Funktionalgleichung
L(x⋅y)=L(x)+L(y)L(x \cdot y) = L(x) + L(y).(1)
Wegen L(1)=L(1⋅1)=L(1)+L(1)L(1)=L(1\cdot 1)=L(1)+L(1) gilt stets L(1)=0L(1)=0. Die stetigen Lösung von (1) sind sogar differenzierbar. Den natürlichen Logarithmus erhält man mit der Zusatzbedingung L′(1)=1L'(1) = 1 oder L(e)=1L(e)=1.
Schließt man die triviale Lösung L(x)=0L(x) = 0 von (1) aus und fordert, dass LL stetig ist, so sind die Logarithmusfunktion genau die Funktionen, die dieser Gleichung genügen.
 
 

Die Mathematik muß man schon deswegen studieren, weil sie die Gedanken ordnet.

M. W. Lomonossow

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen