Trigonometrische Funktionen

Die trigonometrischen Funktionen oder auch Winkelfunktionen (seltener: Kreisfunktionen oder goniometrische Funktionen) basieren auf der Zuordnung zwischen Winkeln und Seitenverhältnissen und wurden ursprünglich an rechtwinkligen Dreiecken definiert.

Inhalt

 
 

Übersicht der trigonometrischen Funktionen

Die trigonometrischen Funktionen sind:
sowie deren Kehrwerte
Zwischen diesen Funktionen bestehen enge Zusammenhänge (siehe Tabelle weiter unten). Genau genommen würde bereits eine der Funktionen ausreichen, um beliebige trigonometrische Probleme lösen zu können. Die Verwendung mehrerer verschiedener Funktionen ermöglicht jedoch eine Vereinfachung der Rechnungen und Formeln.
Die Sekansfunktion und die Kosekansfunktion werden heute kaum noch verwendet.

Definition

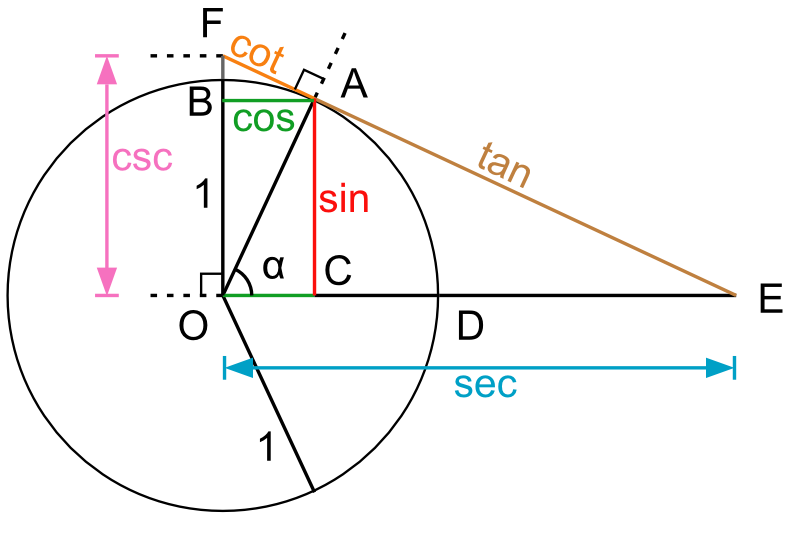
KreisTrig.png
Abb. 1: Definition der Winkelfunktionen am Einheitskreis.
Die Winkelfunktionen können als Sekanten- und Tangentenabschnitte am Einheitskreis definiert werden. Vom Schnittpunkt AA des Winkelschenkels mit dem Einheitskreis werden die Lote (Punkte BB und CC in Abb. 1) auf die beiden Koordinatenachsen gefällt und liefern für den Winkel α\alpha den Sinus als ∣AC‾∣|\ovl{AC}| und Kosinus als ∣AB‾∣|\ovl{AB}|. Die Tangente an den Einheitskreis durch AA schneidet die xx-Achse im Punkt EE und die yy-Achse im Punkt FF; und wir erhalten dann den Tangens ∣AE‾∣|\ovl{AE}| und den Kotangens ∣AF‾∣| \ovl{AF} |. Den Sekans erhält man als ∣OE‾∣| \ovl{OE} | und den Kosekans als ∣OF‾∣|\ovl{OF} |.

Beziehungen zwischen den Funktionen

Der Betrag wird wie folgt umgerechnet:
sin cos tan cot sec csc
sin(x)  sin⁡(x) \,\sin(x) 1−cos⁡2(x) \sqrt{1-\cos^2(x)} tan⁡(x)1+tan⁡2(x) \frac{\tan(x)}{\sqrt{1 + \tan^2(x)}} 1cot⁡2(x)+1 \frac{1}{\sqrt{\cot^2(x) + 1}} sec⁡2(x)−1sec⁡(x) \frac{\sqrt{\sec^2(x)-1}} {\sec(x)} 1csc⁡(x) \frac{1}{\csc(x)}
cos(x)  1−sin⁡2(x) \, \sqrt{1-\sin^2(x)}  cos⁡(x) \, \cos(x)  11+tan⁡2(x) \, \frac{1}{\sqrt{1 + \tan^2(x)}}  cot⁡(x)cot⁡2(x)+1 \, \frac{\cot(x)} {\sqrt{\cot^2(x)+ 1}}  1sec⁡(x) \, \frac{1}{\sec(x)}  csc⁡2(x)−1csc⁡(x) \, \frac{\sqrt{\csc^2(x)-1}}{\csc(x)}
tan(x)  sin⁡(x)1−sin⁡2(x) \, \frac{\sin(x)}{\sqrt{1-\sin^2(x)}}  1−cos⁡2(x)cos⁡(x) \, \frac{\sqrt{1-\cos^2(x)}}{\cos(x)}  tan⁡(x) \, \tan(x)  1cot⁡(x) \, \frac{1}{\cot(x)}  sec⁡2(x)−1 \, \sqrt{\sec^2(x)-1}  1csc⁡2(x)−1 \, \frac{1}{ \sqrt{\csc^2(x)-1}}
cot(x)  1−sin⁡2(x)sin⁡(x) \, \frac{\sqrt{1-\sin^2(x)}}{\sin(x)}  cos⁡(x)1−cos⁡2(x) \, \frac{\cos(x)}{\sqrt{1-\cos^2(x)}}  1tan⁡(x) \, \frac{1}{\tan(x)}  cot⁡(x) \, \cot(x)  1sec⁡2(x)−1 \, \frac{1}{\sqrt{\sec^2(x)-1}}  csc⁡2(x)−1 \, \sqrt{\csc^2(x)-1}
sec(x)  11−sin⁡2(x) \, \frac{1}{\sqrt{1-\sin^2(x)}}  1cos⁡(x) \, \frac{1}{\cos(x)}  1+tan⁡2(x) \, \sqrt{1 + \tan^2(x)}  cot⁡2(x)+1cot⁡(x) \, \frac{\sqrt{\cot^2(x) + 1}}{\cot(x)}  sec⁡(x) \, \sec(x)  csc⁡(x)csc⁡2(x)−1 \, \frac{\csc(x)}{\sqrt{\csc^2(x)-1}}
csc(x)  1sin⁡(x) \, \frac{1}{\sin(x)}  11−cos⁡2(x) \, \frac{1}{\sqrt{1 - \cos^2(x)}}  1+tan⁡2(x)tan⁡(x) \, \frac{\sqrt{1 + \tan^2 (x)}} {\tan(x)}  cot⁡2(x)+1 \, \sqrt{\cot^2(x) + 1}  sec⁡(x)sec⁡2(x)−1 \, \frac{\sec(x)}{\sqrt{\sec^2(x) - 1}}  csc⁡(x) \, \csc(x)

Umkehrung der trigonometrischen Funktionen

Die Umkehrfunktionen der Winkelfunktionen sind die Arkusfunktionen oder inverse Winkelfunktionen arcsin⁡\arcsin, arccos⁡\arccos, arctan⁡\arctan und arccot⁡\arccot . Sie werden verwendet, um aus Seitenverhältnissen Winkel zu berechnen.

Ein guter mathematischer Scherz ist immer besser als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen.

John Edensor Littlewood

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Trigonometrische Funktion aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen