Umkehrfunktionen

Wenn eine Abbildung injektiv ist, ist ihre Umkehrung auch eine Abbildung. Dies gilt analog für reelle Funktionen. Ist eine Funktion auf einem Intervall nicht umkehrbar eindeutig, muss man den Definitionsbereich der Funktion eventuell einschränken, um die Umkehrung der Funktion zu bestimmen.
Für die Umkehrung der Funktion ff schreibt man f −1f\, ^\me.

Beispiele

1) Um die Umkehrfunktion von y=f(x)=2x−2y=f(x)=2x-2 zu bestimmen, stellen wir die Gleichung nach x um und erhalten x=y+22=y2+1x=\dfrac {y+2} 2=\dfrac y 2 +1. Um eine Darstellung der Form y=f(x)y=f(x) zu erhalten, tauschen wir die Namen der Variablen xx und yy aus.
f −1(x)=x2+1f\, ^\me(x)=\dfrac x 2 +1
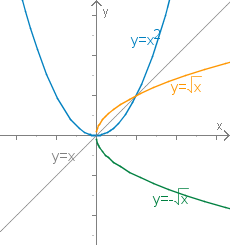
UkFunk.png
2) Die Funktion y=f(x)=x2y=f(x)=x^2 ist auf ganz R\domR definiert dort aber nicht umkehrbar. Sie besitzt zwei Umkehrungen.
f 1−1=xf\, ^\me_1=\sqrt{x} für x≥0x\geq 0 und f 2−1=−xf\, ^\me_2=\uminus\sqrt{x} für x≤0x\leq 0.
Den Graphen der Umkehrfunktion f −1f\, ^\me einer Funktion ff erhält man durch Spiegelung an der Geraden y=f(x)=xy=f(x)=x.

Satz 5726A

Ist eine Funktion f auf einem Intervall II streng monoton, so existiert dort die Umkehrfunktion.

Beweis

Sei ff streng monoton wachsend (für streng monoton fallende Funktionen arbeitet der Beweis analog).
Sei für beliebige x1,x2∈Ix_1,x_2\in I mit x1≠x2x_1\neq x_2. Es gelte x1<x2x_1<x_2 (andernfalls vertauschen wir x1x_1 und x2x_2). Wegen der Monotonie gilt dann aber auch f(x1)<f(x2)f(x_1)<f(x_2) und damit f(x1)≠f(x2)f(x_1)\neq f(x_2). ff ist also injektiv auf II und damit umkehrbar. □\qed
 
 

So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen