Differentialrechnung

Wenn für eine reelle Funktion ff an der Stelle x0x_0 der Grenzwert
d⁡fd⁡x(x0)=f′(x0)=lim⁡x→x0f(x)−f(x0)x−x0\dfrac { \d f}{\d x } (x_0) =f'(x_0)=\lim\limits_{x\rightarrow x_0} \dfrac { f(x)-f(x_0)} {x-x_0}
existiert, dann heißt dieser Differentialquotient oder Ableitung von ff an der Stelle x0x_0. Die Funktion heißt an dieser Stelle differenzierbar oder ableitbar.
Ist eine Funktion ff an jeder Stelle einer Teilmenge M⊆dom(f)M\subseteq\Domain (f) differenzierbar, so heißt sie auf MM differenzierbar. Ist die Ableitung als Funktion betrachtet stetig, so heißt ff stetig differenzierbar.
Eine andere Formulierung der Definition erhalten wir, wenn wir h:=x−x0h:=x-x_0 setzen:
f′(x0)=lim⁡h→0f(x0+h)−f(x0)hf'(x_0)=\lim\limits_{h\rightarrow 0} \dfrac { f(x_0+h)-f(x_0)} {h}
 
 

Beispiel

Die Ableitung von y=f(x)=x2y=f(x)=x^2 an der Stelle x0x_0 ist f ′(x0)=lim⁡h→0f(x0+h)−f(x0)hf\, '(x_0)=\lim\limits_{h\rightarrow 0} \frac { f(x_0+h)-f(x_0)} {h} =lim⁡h→0(x0+h)2−x02h=\lim\limits_{h\rightarrow 0} \frac { (x_0+h)^2-x_0^2} {h} =lim⁡h→0x02+2x0h+h2−x02h=\lim\limits_{h\rightarrow 0} \frac { x_0^2+2x_0h+h^2-x_0^2} {h} =lim⁡h→0(2x0+h)=2x0=\lim\limits_{h\rightarrow 0} (2x_0+h)=2x_0
Die Ableitungsfunktion ist dann y′=2xy'=2x.

Geometrische Deutung

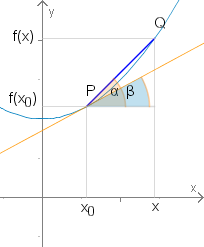
Ableitung.png
Wenn wir uns den Graphen der Funktion ff in der euklidischen Ebene veranschaulichen und die Punkte P=(x0;f(x0))P=(x_0; f(x_0)) und Q=(x;f(x))Q=(x; f(x)) durch eine Gerade verbinden, erhalten wir eine Sekante an den Graphen der Funktion.
Der Differenzenquotient
ΔyΔx=f(x)−f(x0)x−x0=tan⁡α\dfrac {\Delta y}{\Delta x}=\dfrac { f(x)-f(x_0)} {x-x_0}=\tan\alpha
entspricht dem Anstieg dieser Geraden.
Durch den Grenzübergang x→x0x\rightarrow x_0 geht die Sekante in die Tangente an die Kurve im Punkt PP über. Die Ableitung
f ′(x0)=tan⁡βf\, '(x_0)=\tan\beta
ist dann der Anstieg der Tangente an den Graphen der Funktion in diesem Punkt.

Beispiel

Sei die Normalparabel y=f(x)=x2y=f(x)=x^2 gegeben. Wir wollen die Gleichung der Tangenten and die Funktion an der Stelle x0=2x_0=2 bestimmen.
Die Ableitung ist y′=2xy'=2x, die gesuchte Gerade muss also den Anstieg m=2x0=4m=2x_0=4 haben. Wir setzen als Geradengleichung
g(x)=4x+ng(x)=4x+n(1)
an. Um die fehlende Größe nn zu ermitteln, bestimmen wir f(x0)=f(2)=4f(x_0)=f(2)=4 und setzen dies in (1) ein, um
4=4⋅2+n4=4\cdot2+n(2)
zu erhalten. Damit ergibt sich n=−4n=-4 und die gesuchte Geradengleichung ist:
g(x)=4x−4g(x)=4x-4.(3)

So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Funktionen einer Veränderlichen