Funktionsfolgen und Funktionsreihen

Analog zum Begriff der Zahlenfolge, kann man Funktionsfolgen definieren. Dabei handelt es sich um Abbildungen aus der Menge der natürlichen Zahlen in die Menge der Funktionen. Dabei setzt man voraus, dass die Funktionen einen gemeinsamen Definitionsbereich $D$ haben. Man schreibt dann $(f_n)$ für die Funktionsfolge, wobei $f_n:D\rightarrow \dom R$ für alle $n\in\dom N$ gilt.

Den Konvergenzbegriff überträgt man punktweise auf Funktionsfolgen.

Die Funktionsfolge $(f_n)$ konvergiert punktweise gegen eine Funktion $f$, wenn die Zahlenfolge $f_n(x)$ gegen $f(x)$ für alle $x\in D$ konvergiert. Man schreibt dann

.

Die Funktion $f$ heißt dann auch Grenzfunktion der Funktionsfolge $(f_n)$ .

Obwohl diese Übertragung des Konvergenzbegriffes sehr nahe liegend ist, hat er jedoch eine unschöne Eigenschaft: er erhält die Stetigkeit nicht. Eine Folge von stetigen Funktionen kann punktweise gegen eine unstetige Funktion konvergieren, wie das folgende Beispiel zeigt:

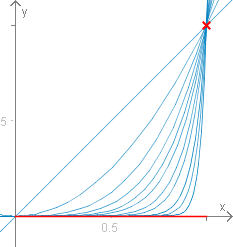
Sei $f_n(x)=x^n$ die für $n\in\dom N$ auf $D=[0,1]$ definierte Funktionsfolge von Potenzfunktionen. Man überzeugt sich leicht, dass diese punktweise gegen die folgende Funktion konvergiert

Diese ist für $x=1$ nicht stetig.