Topologie

Die Topologie oder Analysis situs, wie sie früher meistens genannt wurde, ist ein Teilgebiet der Mathematik. Sie ist im wesentlichen eine Schöpfung des 20. Jahrhunderts und trotzdem bereits seit Jahrzehnten als Grundlagenfach anerkannt. Insofern hat sie (zusammen unter anderem mit der linearen Algebra und der Maßtheorie) das Erbe der Geometrie angetreten.
Gegenstände der Topologie sind in umfassender Weise die topologischen Räume und deren charakteristische topologische Strukturen. Auch diese werden häufig kurz Topologien genannt, die genaue Definition findet sich dort. Topologische Räume können als radikale Verallgemeinerung des „Anschauungsraumes“ der Elementargeometrie verstanden werden, und der erstaunliche Erfolg dieses Konzeptes ist die Folge seiner Fähigkeit, eine Vielzahl von Phänomenen zu integrieren.
Die Topologie als Teilgebiet lässt sich noch weiter unterteilen in mengentheoretische Topologie, die sich allgemein mit topologischen Räumen beschäftigt, und algebraische Topologie, die diejenigen Eigenschaften von topologischen Räumen untersucht, die unter stetigen Abbildungen erhalten bleiben.

Einführung

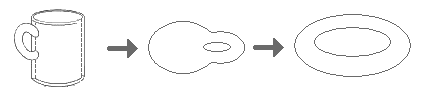
Die Topologie untersucht die Eigenschaften geometrischer Körper (d. h. topologischer Räume), die durch Verformungen mit Homöomorphismen nicht verändert werden. Dazu gehört das Dehnen, Stauchen, Verbiegen, Verzerren, Verdrillen eines Gegenstands; das Zerschneiden aber nur, wenn man ihn später an genau der Schnittfläche wieder zusammenklebt. Zum Beispiel haben eine Kugel und ein Glas dieselbe Topologie; sie sind homöomorph. Ebenso sind ein Torus und eine einhenkelige Tasse homöomorph.
Homoeo_tasse.png
Der axiomatische Aufbau der modernen Topologie beruht auf dem grundlegenden Konzept der "Nachbarschaft", formalisiert als offene Umgebung. Neben offen und abgeschlossen gibt es als weitere fundamentale topologische Begriffe stetig, kompakt, separabel, zusammenhängend, dicht, Rand, Inneres, Weg. Neben der Algebra kann die Topologie als zweiter Stützpfeiler für alle anderen Felder der Mathematik angesehen werden; sie ist besonders wichtig für die Geometrie, die Analysis (Maß- und Integrationstheorie), die Funktionalanalysis, die Theorie der Lie-Gruppen, die Graphentheorie usw.
Untergebiete der Topologie sind die algebraische Topologie, die Differentialtopologie.

Exaktere Darstellung

Die Topologie formalisiert den Begriff der "Nähe" (besser: Umgebung. Oder: infinitesimale Nähe).
Als Beispiel betrachte man z. B. die topologischen Räume der ganzen Zahlen Z\mathbb{Z} und die der rationalen Zahlen Q\mathbb{Q} (mit der aus der Metrik induzierten Topologie). Da es bijektive Abbildungen zwischen Z\mathbb{Z} und Q\mathbb{Q} gibt, sind sie gleichmächtig. Sie sind also als Mengen ununterscheidbar, solange man sie nur als Ansammlung von Elementen betrachtet, ohne deren Eigenschaften und Beziehungen zu berücksichtigen. Aber die beiden Mengen unterscheiden sich hinsichtlich ihrer topologischen Struktur: In Z\mathbb{Z} liegen alle Punkte isoliert, d. h. im Gegensatz zu Q\mathbb{Q} gibt es um jeden Punkt eine kleine Umgebung, in der kein weiterer Punkt liegt. Deshalb gibt es keinen Homöomorphismus zwischen beiden.
In unserem Beispiel kann man für je zwei Punkte aus Z\mathbb{Z} oder Q\mathbb{Q} den Abstand angeben. Eine Umgebung eines Punktes pp besteht mindestens aus all den Punkten, deren Abstand zu pp kleiner als eine Zahl cc ist. Auf den ganzen Zahlen gibt es also kleine Umgebungen, die keinen weiteren Punkt enthalten, während für die rationalen Zahlen jede Umgebung eines Punktes unendlich viele weitere Elemente aus Q\mathbb{Q} enthält, unabhängig davon, wie klein die Zahl cc und damit die Umgebung gewählt wird.
Während die beiden obigen Beispiele den Begriff des Abstandes verwenden, besteht die Leistung der (mengentheoretischen) Topologie darin, das Konzept der Nähe auf den Kern reduziert zu haben.
Dies gelingt, indem man statt der Abstandsfunktion nur noch die Menge aller Umgebungen betrachtet (bzw. in einer beliebigen Menge MM zu jedem Punkt einen Satz von Teilmengen auswählt, die man als die Umgebungen dieses Punktes definiert). Man findet so viele Beispiele von topologischen Räumen, auf denen es nicht mehr möglich ist, den Abstand zwischen den Punkten anzugeben.
Es gibt zwei Gründe, die für die Betrachtung dieser Struktur sprechen: Zunächst gibt es natürliche Beispiele von Räumen, auf denen keine Abstandsfunktion definiert werden kann (z. B. manche Quotientenräume). Andererseits ist man oft nicht an dem konkreten Abstand interessiert: Man stelle sich einen Körper im R3\mathbb{R}^3 vor, den man ausbeult und verformt (ohne ihn aber zu zerreißen). Der Abstand zweier Punkte in diesem Objekt hat sich geändert, aber wichtige Grundeigenschaften sind geblieben, z. B. kann man zwei Punkte, die man vor der Verformung verbinden konnte, auch weiterhin verbinden, oder ein Punkt im Innern des Körpers bleibt im Innern.
Nicht jede Abbildung zwischen topologischen Räumen ist verträglich mit der zusätzlichen Struktur (z.B. gibt es bijektive Abbildungen zwischen den ganzen und den rationalen Zahlen, aber die beiden Räume sehen ganz verschieden aus). Eine Abbildung ist in diesem Sinne gutartig und wird stetig genannt, „wenn sie die Nähe erhält“. Eine Funktion f:R→Rf:\mathbb{R}\to\mathbb{R}, die x≠0x\ne 0 auf 00 und 00 auf 11 abbildet, ist z. B. nicht stetig, denn Zahlen, die "in der Nähe von 00 liegen", werden "weit weg" von f(0)f(0) abgebildet.
Die mengentheoretische Topologie erlaubt die Konstruktion von sehr vielen Pathologien. Dies macht sie in der größten Allgemeinheit zu einem relativ fruchtlosen Gebiet. Topologen beschäftigen sich deshalb mit spezielleren Räumen, z. B. Mannigfaltigkeiten oder CW-Komplexen.

Literatur

  • N. Bourbaki: Topologie générale, Hermann (1961).
  • T. Camps, S. Kühling, G. Rosenberger: Einführung in die mengentheoretische und die algebraische Topologie, Heldermann 2006, ISBN 388538115X.
  • H. Herrlich: Topologie I: Topologische Räume, Heldermann 1986, ISBN 3885381028.
  • Kazimierz Kuratowski: Topologie I, 1933
  • H. Schubert: Topologie, Teubner, Stuttgart 1964, ISBN 3519122006
  • Allen Hatcher: Algebraic Topology. Cambridge University Press 2000 ISBN 0-521-79540-0
  • Boto v. Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer, Berlin 2001, ISBN 3540677909
 
 

Nicht etwa, daß bei größerer Verbreitung des Einblickes in die Methode der Mathematik notwendigerweise viel mehr Kluges gesagt würde als heute, aber es würde sicher viel weniger Unkluges gesagt.

Karl Menger

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Topologie (Mathematik) aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung