Bijektion, Bijektivität

Eine Abbildung f:A→Bf:A \rightarrow B heißt Bijektion oder bijektive Abbildung genau dann, wenn ff injektiv und surjektiv ist. Damit ist ff eine eineindeutige Auf-Abbildung. Jedem Element aus AA wird genau ein Element aus BB zugeordnet und alle Elemente aus BB kommen als Bilder vor.
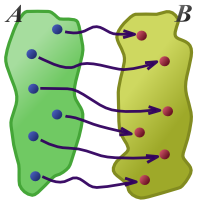
Bijektiv.png
Grafische Veranschaulichung einer Bijektion
Betrachten wir jetzt die bijektiven Abbildungen einer Menge MM auf sich. Dann gibt es eine ausgezeichnete Bijektion id⁡\id, die identische Abbildung oder identische Funktion: id⁡(a):=a\id(a):=a.
Weiterhin halten wir fest, dass die Hintereinanderausführung zweier Bijektionen wieder eine Bijektion ist sowie dass die Umkehrung einer Bijektion eine Bijektion ist. Es gilt:
 
 

Satz 15XJ (Eigenschaften bijektiver Abbildungen)

Seien f:A→Bf:A\rightarrow B und g:B→Cg:B\rightarrow C bijektive Abbildungen. Dann gilt:
  1. Die Hintereinanderausführung g∘fg\circ f ist bijektiv.
  2. Die Umkehrabbildung f−1f^{\me} ist bijektiv

Beweis

Lässt sich durch Anwendung der Definition schnell überprüfen. □\qed
Wir bemerken noch, dass alle Bijektionen einer Menge MM auf sich bezüglich der Hintereinanderausführung ∘\circ eine Gruppe bilden, die symmetrische Gruppe. Neutrales Element ist die identische Abbildung id⁡\id. Ist MM endlich spricht man auch von Permutationen.

Beispiele

Die Funktion f1(x)=xf_1(x)=x ist bijektiv auf R\domR. Die Funktion f2(x)=x2f_2(x)=x^2 ist nicht bijektiv auf R\R jedoch als Abbildung f2:[0,∞[→[0,∞[f_2:[0,\infty[\to[0,\infty[ betrachtet bijektiv.
Oft ist folgendes Lemma nützlich

Lemma 5212C

Sei f:A→Bf:A \rightarrow B eine injektive Abbildung, dann ist die Einschränkung f:A→f(A)f:A \rightarrow f(A) eine Bijektion.
Natürlich ist dann auch f −1:f(A)→Af\, ^{-1}: f(A)\rightarrow A eine Bijektion.

Beweis

Sei b∈f(A)b\in f(A) damit gibt es nach Definition von f(A)f(A) ein a∈Aa\in A mit f(a)=bf(a)=b und damit ist ff surjektiv. □\qed

Satz B6HE

Seien f:A→Bf:A\to B und g:B→Ag:B\to A zwei Abbildungen, deren Komposition die identische Abbildung ergibt (g∘f=id⁡Ag\circ f=\id_A). Dann ist ff injektiv und gg surjektiv.

Beweis

Für a1,a2∈Aa_1,a_2\in A sei f(a1)=f(a2)f(a_1)=f(a_2)   ⟹  g(f(a1))=g(f(a2))\implies g(f(a_1))=g(f(a_2))   ⟹  a1=a2\implies a_1=a_2.
Für die Surjektivität von gg müssen wir zeigen, dass es für alle a∈Aa\in A ein b∈Bb\in B gibt mit g(b)=ag(b)=a. Nun leistet b=f(a)b=f(a) aber gerade das Geforderte. □\qed

Folgerung JJ25

Seien f:A→Bf:A\to B und g:B→Ag:B\to A zwei Abbildungen, deren wechselseitige Komposition die identische Abbildung ergibt (g∘f=id⁡Ag\circ f=\id_A und f∘g=id⁡Bf\circ g=\id_B). Dann sind sowohl ff als auch gg bijektiv.

Beweis

Man wende Satz B6HE zweifach an, dann sind ff und gg injektiv und surjektiv, also bijektiv. □\qed

Alle Pädagogen sind sich darin einig: man muß vor allem tüchtig Mathematik treiben, weil ihre Kenntnis fürs Leben größten direkten Nutzen gewährt.

Felix Klein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre