Surjektion, Surjektivität

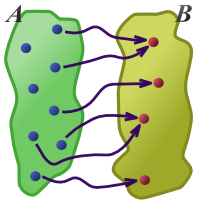
Surjektiv.png
Surjektion: Alle Elemente aus BB kommen als Bilder vor
Wenn bei einer Abbildung f:A→Bf: A\rightarrow B die Bildmenge mit BB zusammenfällt also Wf=BW_f = B gilt, so heißt ff surjektiv oder Aufabbildung. Jedes Element aus BB kommt als Element wenigstens eines Elementes aus AA vor.
ff surjektiv   ⟺  ∀y∈B∃x∈A:f(x)=y\iff \forall y\in B\quad \exists x\in A : f(x) =y
Die Grafik verdeutlicht das Wesen der Surjektivität: Alle Werte aus BB werden als Funktionswerte angenommen, was dadurch symbolisiert wird, dass sie von einem Pfeil erreicht werden.

Beispiele

Die lineare Funktion f1(x)=xf_1(x)=x ist surjektiv auf R\domR.
Die quadratische Funktion f2(x)=x2f_2(x)=x^2 ist nicht surjektiv auf R\R, denn negative Zahlen werden nicht als Funktionswerte angenommen. Schränkt man den Wertebereich auf das Intervall [0,∞[[0,\infty[ ein, so ist die Funktion auf diesem Intervall surjektiv.
Allgemein kann man aus einer beliebigen Funktion ff eine surjektive Funktion machen, wenn man ihren Wertebereich auf die tatsächlich angenommen Werte einschränkt.

Eigenschaften

Die Surjektivität einer Funktion f ⁣: A→Bf\colon\, A \to B hängt nicht nur vom Funktionsgraphen {(x,f(x))∣x∈A},\{(x,f(x)) \mid x \in A\}, sondern auch von der Zielmenge BB abhängt (im Gegensatz zur Injektivität, welche man am Funktionsgraphen ablesen kann).
Eine Funktion f ⁣: A→Bf\colon\, A \to B ist genau dann surjektiv, wenn f(f−1(Y))=Yf\big(f^{-1}(Y) \big)=Y für alle Y⊂B Y \subset B .
Sind die Funktionen f ⁣: A→Bf\colon\, A \to B und g ⁣: B→Cg\colon\, B \to C surjektiv, dann gilt dies auch für die Komposition (Verkettung) g∘f ⁣: A→C.g \circ f\colon\, A \to C.
Aus der Surjektivität von g∘fg \circ f folgt, dass gg surjektiv ist.
Eine Funktion f ⁣: A→Bf\colon\, A \to B ist genau dann surjektiv, wenn ff eine Rechtsinverse hat, also eine Funktion g ⁣: B→Ag\colon\, B \to A mit f∘g=id⁡Bf \circ g = \operatorname{id}_B (wobei id⁡B\operatorname{id}_B die identische Abbildung auf BB bezeichnet).
Eine Funktion f:A→Bf : A \to B ist genau dann surjektiv, wenn ff rechtskürzbar ist, also für beliebige Funktionen g,h:B→Cg, h : B \to C mit g∘f=h∘fg \circ f = h \circ f schon g=hg = h folgt.
Jede beliebige Funktion f ⁣: A→Bf\colon\, A \to B ist darstellbar als Verkettung f=h∘gf = h \circ g, wobei gg surjektiv und hh injektiv ist. g ⁣: A→im⁡fg\colon\, A \to \operatorname{im} f hat dabei die Bildmenge von ff als Zielmenge und stimmt ansonsten mit ff überein.
 
 

Manche Menschen haben einen Gesichtskreis vom Radius Null und nennen ihn ihren Standpunkt.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Surjektivität aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre