Injektive Abbildungen

Injektiv.png
Eine Abbildung f:A→Bf:A \rightarrow B, deren Umkehrung f−1f^{-1} wieder eindeutig ist, nennt man eineindeutig oder umkehrbar eindeutig oder injektiv. Bei einer injektiven Abbildung gibt es zu jedem Element b∈Bb\in B höchstens ein Element a∈Aa\in A mit b=f(a)b=f(a).
ff injektiv   ⟺  ∀x1,x2:f(x1)=f(x2)  ⟹  x1=x2\iff \forall x_1,x_2: f(x_1)=f(x_2)\implies x_1=x_2
Eine äquivalente Formulierung ist x1≠x2  ⟹  f(x1)≠f(x2)x_1\neq x_2 \implies f(x_1)\neq f(x_2).
Die Injektivität fordert nicht, dass alle Elemente aus BB als Bilder vorkommen müssen. (Dann wäre die Funktion surjektiv).
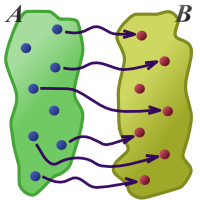
Die nebenstehende Grafik verdeutlicht das Wesen der Injektivität. Zu keinem Wert aus BB gehen zwei Pfeile.
Die Bezeichnung umkehrbar eindeutig drückt aus, dass die Umkehrung einer injektiven Abbildung ff wieder eine Abbildung ist. Diese heißt Umkehrabbildung und wird mit f−1f^\me bezeichnet. Wenn ff nicht injektiv ist, muss die Umkehrung nicht eindeutig sein und damit keine Abbildung.

Beispiele

Die lineare Funktion f1(x)=xf_1(x)=x ist injektiv auf R\domR.
Die quadratische Funktion f2(x)=x2f_2(x)=x^2 ist nicht injektiv auf R\domR, denn jedem xx wird der gleiche Funktionswert wie −x\uminus x zugeordnet. Schränkt man den Definitionsbereich von f2f_2 auf das Intervall [0,∞[[0,\infty[ ein, so ist die Funktion auf diesem Intervall injektiv.

Eigenschaften

Die Injektivität einer Funktion f ⁣:A→Bf\colon A \to B hängt nur vom Funktionsgraphen {(x,f(x))∣x∈A}\{(x, f(x)) \mid x \in A\} abhängt (im Gegensatz zur Surjektivität, die auch von der Bildmenge BB abhängt, die man am Funktionsgraphen nicht ablesen kann). Eine Funktion f ⁣:A→Bf\colon A \to B ist genau dann injektiv, wenn für alle Teilmengen X,Y⊆AX, Y \subseteq A gilt: f(X∩Y)=f(X)∩f(Y)f(X \cap Y)=f(X) \cap f(Y) (Satz 5212B) Eine Funktion f ⁣:A→Bf\colon A \to B ist genau dann injektiv, wenn f−1(f(T))=Tf^{-1}(f(T))=T für alle T⊆AT \subseteq A gilt. Sind die Funktionen f ⁣:A→Bf\colon A \to B und g ⁣:B→Cg\colon B \to C injektiv, dann ist auch die Komposition (Verkettung) g∘f ⁣:A→Cg \circ f\colon A \to C injektiv.
Aus der Injektivität von g∘fg \circ f folgt, dass ff injektiv ist.
Eine Funktion f ⁣:A→Bf\colon A \to B mit nichtleerer Definitionsmenge AA ist genau dann injektiv, wenn ff eine Linksinverse hat, das ist eine Funktion g ⁣:B→Ag\colon B \to A mit g∘f=id⁡Ag \circ f = \operatorname{id}_A (wobei id⁡A\operatorname{id}_A die identische Abbildung auf AA bezeichnet).
Eine Funktion f ⁣:A→Bf\colon A \to B ist genau dann injektiv, wenn sie linkskürzbar ist, wenn also für beliebige Funktionen g,h ⁣:C→Ag, h\colon C \to A aus f∘g=f∘hf \circ g = f \circ h die Gleichheit g=hg = h folgt.
Jede beliebige Funktion f ⁣:A→Bf\colon A \to B ist als Verkettung f=h∘gf = h \circ g darstellbar, wobei gg surjektiv und hh injektiv (nämlich eine Inklusionsabbildung) ist.
Eine stetige reellwertige Funktion auf einem reellen Intervall ist genau dann injektiv, wenn sie in ihrem ganzen Definitionsbereich streng monoton steigend oder streng monoton fallend ist.
Die Injektivität hängt vom Definitionsbereich der Funktion ab.

Anzahl injektiver Abbildungen

Die Anzahl der injektiven Abbildungen von einer Definitionsmenge AA in eine gegebene endliche Zielmenge BB mit der Eigenschaft ∣B∣≥∣A∣|B| \geq |A| ist gegeben durch:
∣B∣⋅(∣B∣−1)⋅…⋅(∣B∣−∣A∣+1)|B|\cdot (|B|-1) \cdot \ldots \cdot (|B|-|A|+1) =∣B∣!(∣B∣−∣A∣)!= \dfrac{|B|!}{(|B|-|A|)!} =∣A∣!⋅(∣B∣∣A∣)= |A|! \cdot \binom{|B|}{|A|}
Dies entspricht in der Kombinatorik einer Variation ohne Wiederholung.
 
 

Im großen Garten der Geometrie kann sich jeder nach seinem Geschmack einen Strauß pflücken.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Injektivität aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Mengenlehre