Umgebungen

Die Teilmenge
Uϵ(x)={y∈M ∣ d(x,y)<ϵ}U_\epsilon(x) =\{y\in M\, |\space d(x,y)<\epsilon\}
heißt ϵ\epsilon-Umgebungdes Puntkes xx. Andere Schreibweisen sind Bϵ(x)B_\epsilon(x) (BB für ball) oder K(x,ϵ)K(x,\epsilon) für offene Kugel um xx mit dem Radius ϵ\epsilon.
Eine Teilmenge UU heißt Umgebung von xx, wenn es ein ϵ>0\epsilon>0 gibt mit Uϵ(x)⊆UU_\epsilon(x)\subseteq U. Um die Umgebungseigenschaft zu kennzeichnen schreiben wir dann U(x)U(x)

Beispiele

In R\domR sind die ϵ\epsilon-Umgebungen die offenen Intervalle der Form ]a−ϵ,a+ϵ[]a-\epsilon,a+\epsilon[.
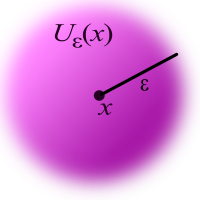
EpsUmg.png
ϵ\epsilon-Umgebungen im R2\R^2
Im Rn{\dom R}^n mit der euklidischen Metrik sind die ϵ\epsilon-Umgebungen um xx genau die (Hyper)-Kugeln mit dem Mittelpunkt xx Radius ϵ\epsilon. Bei der Maximummetrik handelt es sich um Würfel mit der Kantenlänge 2ϵ2\epsilon.

Satz 16RB (Eigenschaften von Umgebungen)

Für jede Umgebung U(x)U(x) gilt:
  1. Ist UU Umgebung von xx, so gilt x∈Ux\in U
  2. Gilt V⊇U(x)V\supseteq U(x), so ist VV Umgebung von xx
  3. Sind UU und VV Umgebungen von xx, so auch U∩VU\cap V (Mittels vollständiger Induktion erweitert man diese Behauptung auf endlich viele Mengen)
  4. Ist UU eine Umgebung von xx, so gibt es eine Umgebung V(x)V(x), so dass für alle y∈V(x)y\in V(x) UU Umgebung von yy ist. Damit gilt auch V(x)⊆U(x)V(x)\subseteq U(x)
Obwohl die Aussagen des Satzes trivial erscheinen, haben sie jedoch eine gewisse theoretische Bedeutung. Baut man die Theorie der topologischen Räume auf den Umgebungsbegriff auf, so sind dies die dafür erforderlichen Axiome. Alle Sätze, deren Beweis auf diesen Satz beruhen, können dann für topologische Räume ohne erneuten Beweis übernommen werden.

Beweis

(i) wegen x∈Uϵ(x)⊆Ux\in U_\epsilon(x)\subseteq U. (ii) wegen x∈Uϵ(x)⊆U⊆Vx\in U_\epsilon(x)\subseteq U\subseteq V. (iii) es existieren δ,ϵ>0\delta,\epsilon>0 mit Uϵ(x)⊆UU_\epsilon(x)\subseteq U und Uδ(x)⊆VU_\delta(x)\subseteq V. Setze γ=min⁡{ϵ,δ}\gamma=\min\{\epsilon,\delta\}. Für z∈Uγ(x)z\in U_\gamma(x) gilt
d(z,x)<γ<=ϵd(z,x)<\gamma<=\epsilon   ⟹  z∈Uϵ(x)⊆U \implies z\in U_\epsilon(x)\subseteq U und
d(z,x)<γ<=δd(z,x)<\gamma<=\delta   ⟹  z∈Uδ(x)⊆V \implies z\in U_\delta(x)\subseteq V,
  ⟹  z∈U∩V\implies z\in U\cap V   ⟹  Uγ(x)⊆U∩V\implies U_\gamma(x)\subseteq U\cap V .
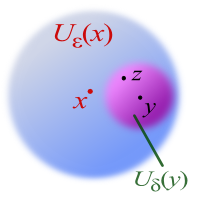
BewUOffen.png
(iv) es existiert ϵ>0\epsilon>0 mit Uϵ(x)⊆UU_\epsilon(x)\subseteq U. Setze V:=Uϵ(x)V:=U_\epsilon(x). Für einen Punkt y∈Uϵ(x)y\in U_\epsilon(x) wählen wir δ=ϵ−d(x,y)\delta=\epsilon - d(x,y). Dann gilt sicher δ>0\delta>0. Wenn z∈Uδ(y)z\in U_\delta(y), dann gilt d(x,z)≤d(x,y)+d(y,z)d(x,z)\leq d(x,y)+d(y,z) <d(x,y)+δ< d(x,y)+\delta =d(x,y)+ϵ−d(x,y)=ϵ= d(x,y)+\epsilon - d(x,y)=\epsilon. Damit ist Uδ(y)⊆Uϵ(x)=V⊆UU_\delta(y)\subseteq U_\epsilon(x)=V\subseteq U und die Behauptung gezeigt. □\qed

Bemerkung 16RE

Der Beweis von (iv) zeigt außerdem, dass eine ϵ\epsilon-Umgebung mit einem Punkt immer eine ganze Umgebung um diesen enthält.
 
 

Ein guter mathematischer Scherz ist immer besser als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen.

John Edensor Littlewood

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Topologie