Metrische Räume

Sei MM eine Menge, dann heißt eine Abbildung d:M×M→Rd: M\cross M \rightarrow \dom R Metrik genau dann, wenn folgende Eigenschaften gelten:
  1. d(x,y)=0   ⟺   x=yd(x,y)=0 \, \iff \, x=y
  2. d(x,y)=d(y,x)d(x,y)=d(y,x) für alle x,y∈Mx,y\in M
  3. d(x,y)≤d(x,z)+d(z,y)d(x,y)\leq d(x,z)+d(z,y) für alle x,y,z∈Mx,y,z\in M
MM versehen mit einer Metrik wird metrischer Raum genannt und mit (M,d)(M,d) bezeichnet. Die Funktion dd ist eine Abstandsfunktion. Für zwei Elemente aus MM, die auch Punkte genannt werden, spricht man dann auch von ihrem Abstand bezüglich der Metrik dd.
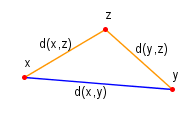
dugl.png
Die Bedingung (iii) ist aus der Elementargeometrie als Dreiecksungleichung bekannt und entspricht der anschaulichen Vorstellung, dass ein Umweg niemals kürzer ist als der direkte Weg.

Bemerkung

Aus der obigen Definition kann man sofort folgern, dass
d(x,y)≥0d(x,y)\geq 0
für alle Punkte eines (halb)metrischen Raums gilt. Es gilt nämlich: 0=d(x,x)≤d(x,y)+d(y,x)=2d(x,y)0=d(x,x)\leq d(x,y)+d(y,x)=2d(x,y).

Satz 5608A (Vierecksungleichung)

In einem (halb)metrischen Raum MM gilt für alle x,y,u,v∈Mx,y,u,v\in M:
∣d(x,y)−d(u,v)∣≤d(x,u)+d(y,v)|d(x,y)-d(u,v)|\leq d(x,u)+d(y,v)

Beweis

Es gilt: d(x,y)≤d(x,u)+d(u,v)+d(v,y)d(x,y)\leq d(x,u)+d(u,v)+d(v,y) und damit d(x,y)−d(u,v)≤d(x,u)+d(v,y)d(x,y)-d(u,v)\leq d(x,u)+d(v,y). Andererseits gilt d(u,v)≤d(u,x)+d(x,y)+d(y,v)d(u,v)\leq d(u,x)+d(x,y)+d(y,v) und damit d(u,v)−d(x,y)≤d(u,x)+d(y,v)d(u,v)-d(x,y)\leq d(u,x)+d(y,v). Aus beiden Ungleichungen ergibt sich die Behauptung. □\qed
 
 

Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis.

Jean-Baptist le Rond d'Alembert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analysis