Beispiele zur Differenzierbarkeit

Beispiel 15JF

Für f(x)=2xx−1f(x)=\dfrac {2x}{x-1} ermitteln wir mit der Quotientenregel:
f ′(x)=2(x−1)−2x(x−1)2=−2(x−1)2f\, '(x)=\dfrac{2(x-1)-2x}{(x-1)^2}=\dfrac{\uminus 2}{(x-1)^2}.
für g(x)=x+1x−1g(x)=\dfrac {x+1}{x-1} erhalten wir als Ableitung:
g′(x)=1⋅(x−1)−(x+1)(x−1)2=−2(x−1)2g'(x)=\dfrac{1\cdot(x-1)-(x+1)}{(x-1)^2}=\dfrac{\uminus 2}{(x-1)^2}.
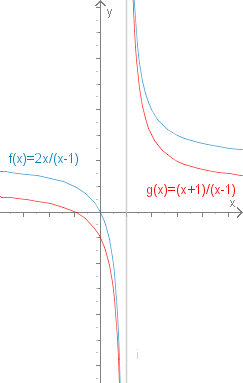
AblGleich.png
Obwohl die Funktionen keineswegs gleich aussahen, haben sie die gleiche Ableitung. Wir vermuten daher, dass sie sich nur um eine Konstante unterscheiden (deren Ableitung verschwindet). Und tatsächlich ist:
f(x)−g(x)=2xx−1−x+1x−1=x−1x−1=1f(x)-g(x)=\dfrac {2x}{x-1}-\dfrac {x+1}{x-1}=\dfrac {x-1}{x-1}=1
für x≠1x\neq1, einer Stelle, an der die Funktionen sowieso nicht differenzierbar waren.
Anhand der Graphen der Funktionen ist dieser Zusammenhang sofort ersichtlich.
 
 

Beispiel

Die Ableitung einer geraden Funktion ist ungerade und die einer ungeraden Funktion gerade.
Es gilt f ′(−x)=−f ′(−x)f\, '(-x)=-f\, '(-x) Damit folgt mit der geraden Funktion aus f(−x)=f(x)f(-x)=f(x) nach dem Differenzieren: −f ′(−x)=f ′(−x)=f ′(x)-f\, '(-x)=f\, '(-x)=f\, '(x). Die Ableitung ist also ungerade. Analog schließt man für ungerade Funktionen.

Alles, was lediglich wahrscheinlich ist, ist wahrscheinlich falsch.

Rene Descartes

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen