Grenzwerte reeller Funktionen

Sei eine reelle Funktion ff in der Umgebung einer Stelle x0x_0 definiert (sie muss nicht unbedingt an der Stelle x0x_0 definiert sein). Dann hat ff an der Stelle x0x_0 den Grenzwert aa, geschrieben lim⁡x→x0f(x)=a\lim_{x\rightarrow x_0} f(x)=a, wenn es zu jedem ϵ>0\epsilon>0 ein δ>0\delta>0 gibt, so dass für alle xx mit ∣x−x0∣<δ|x-x_0|<\delta gilt: ∣f(x)−a∣<ϵ|f(x)-a|<\epsilon. Formal aufgeschrieben:
lim⁡x→x0f(x)=a    ⟺    ∀ϵ>0∃δ>0∀x:∣x−x0∣<δ  ⟹  ∣f(x)−a∣<ϵ\lim_{x\rightarrow x_0} f(x)=a\;\iff\; \forall \epsilon>0\exists \delta>0 \forall x: |x-x_0|<\delta\implies |f(x)-a|<\epsilon
Anschaulich bedeutet der Grenzwert, dass wenn die Argumente nahe bei x0x_0 liegen, dann liegt der Funktionswert auch nahe bei aa.
 
 

Beispiel 15J5

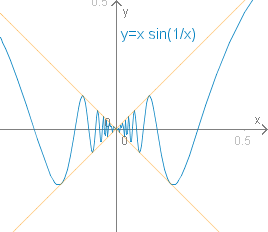
xsin1durchx.png
Wir betrachten die Funktion
f(x)=x⋅sin⁡1xf(x)=x\cdot \sin\dfrac 1 x.
Diese Funktion ist für x0=0x_0=0 nicht definiert. Anhand des Graphen der Funktion liegt die Vermutung nahe, dass
lim⁡x→0f(x)=lim⁡x→0x⋅sin⁡1x=0\lim_{x\rightarrow 0} f(x) =\lim_{x\rightarrow 0}x\cdot \sin\dfrac 1 x=0(1)
gilt.
Sei ϵ>0\epsilon>0 gegeben. Wir müssen jetzt ein δ>0\delta>0 finden, so dass aus
∣x−0∣=∣x∣<δ|x-0|=|x|<\delta(2)
folgt, dass
∣f(x)−0∣=∣x⋅sin⁡1x∣<ϵ|f(x)-0|=\ntxbraceI{x\cdot \sin\dfrac 1 x}<\epsilon(3)
gilt.
Es ist ∣x⋅sin⁡1x∣=∣x∣⋅∣sin⁡1x∣\ntxbraceI{x\cdot \sin\dfrac 1 x}=|x|\cdot \ntxbraceI {\sin\dfrac 1 x} und ∣sin⁡x∣≤1|\sin x|\leq 1 wegen der Definition des Sinus.
Damit gilt ∣x⋅sin⁡1x∣≤∣x∣\ntxbraceI{x\cdot \sin\dfrac 1 x}\leq |x| und wegen (2) brauchen wir nur ϵ=δ\epsilon=\delta zu setzen, um (3) zu erfüllen. Damit ist (1) gezeigt.

Die Mathematik als Fachgebiet ist so ernst, daß man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.

Blaise Pascal

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Funktionen einer Veränderlichen