Beispiele zu Funktionsgrenzwerten

Beispiel 5319A

Ausgehend von der Definition von

\lim_{x\rightarrow\infty}{\braceNT{1+\dfrac 1 x}}^x=\e

erhalten wir mit der Substitution

x=\dfrac 1 a

{\lim_{a\rightarrow 0}} {({1+a})^{1/a}}=\e

und wenn wir auf beiden Seiten logarithmieren ergibt sich

\lim_{a\rightarrow 0} \dfrac {\ln(1+a)} a=1

Mit einer weiteren Substitution

b=\e^a-1

erhalten wir den Grenzwert

\lim_{b\rightarrow 0} \dfrac {b} {\e^b-1}=1

den wir auch als

\lim_{x\rightarrow 0} \dfrac {\e^x-1} {x} =1

schreiben können.

\lim_{x\rightarrow 0}\dfrac {\sin x} x

zu bestimmen, machen wir zuerst eine Vorüberlegung.

Für

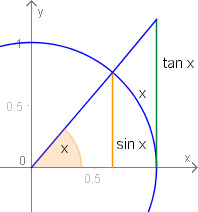
x\in [0,\dfrac \pi 2[

entnimmt man der Skizze sofort die Gültigkeit der Ungleichung

\sin x\leq x\leq \tan x

Damit gilt dann aber

\sin x\leq x\leq \dfrac {\sin x}{\cos x}

und für

x>0

erhalten wir

\dfrac {\cos x}{\sin x}\leq \dfrac 1 x\leq \dfrac 1{\sin x}

und nach Multiplikation mit

\sin x

erhalten wir folgende Ungleichung

\cos x\leq \dfrac {\sin x} x\leq 1

Mit dem Grenzübergang ergibt sich:

1=\lim_{x\rightarrow +0}\cos x

\leq \lim_{x\rightarrow +0}\dfrac {\sin x} x\leq 1

was nichts anderes bedeutet, als dass der gesuchte Grenzwert

1

ist.

Bei diesen Überlegungen haben wir eigentlich nur den rechtsseitigen Grenzwert bestimmt, man kann jedoch analoge Überlegungen auch für

x<0

durchführen; mithin gilt also:

\lim_{x\rightarrow 0}\dfrac {\sin x} x=1

Es gibt keinen Königsweg zur Mathematik.

Euklid

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе