Asymptoten

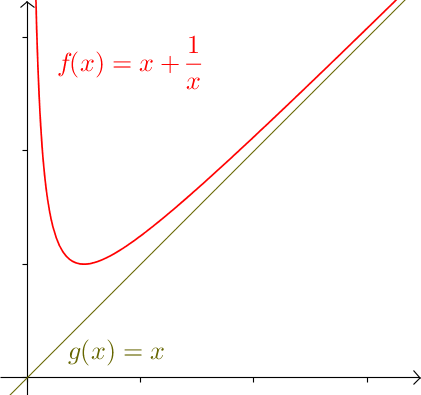
asym1.png
Die rot dargestellte Funktion f(x)=1x+xf(x) = \dfrac{1}{x}+x besitzt die Asymptote g(x)=xg(x) = x
Eine Asymptote bezeichnet eine Gerade oder allgemein auch eine eine Kurve, die sich einer vorgegebenen Funktion in einem Grenzprozess beliebig annähert.
Zwei Funktionen ff und gg heißen asymptotisch äquivalent, wenn für den Grenzwert ihres Quotienten gilt:
lim⁡x→∞f(x)g(x)=1\lim_{x\to\infty}\dfrac{ f(x)}{g(x)}=1
Eine Funktion und ihre Asymptote sind also asymptotisch äquivalent. In der [!Abbildung] sind also f(x)=1x+xf(x)=\dfrac{1}{x}+x und g(x)=xg(x) = x asymptotisch äquivalent.
 
 

Asymptoten einer Funktion

Eine Asymptote ist ein Graph (zum Beispiel eine Gerade), der sich dem Graphen einer gegebenen Funktion beliebig weit annähert. Asymptoten von Funktionen betrachtet man insbesondere im Rahmen einer Kurvendiskussion.
Gegeben sei eine Funktion f: D→Rf: \ D\to\R mit D⊂RD\subset\R. Man unterscheidet zwischen zwei verschiedenen Typen von Asymptoten, da sich eine Funktion entweder in x- oder in y-Richtung annähern kann.

Annäherung in y-Richtung

Hat ff an der Stelle tt eine Polstelle, d. h. gilt
lim⁡x→+tf(x)=±∞  \lim_{x\to +t} f(x) = \pm\infty\,\, oder   lim⁡x→−tf(x)=±∞,\,\,\lim_{x\to -t} f(x) = \pm\infty,
dann nennt man die Gerade x=t x = t eine senkrechte (oder vertikale) Asymptote von ff oder eine Polgerade von ff.

Annäherung in x-Richtung

Konvergiert ff für xx gegen ∞\infty gegen eine reelle Zahl hh, d. h. gilt
lim⁡x→∞f(x)=h\lim_{x\to \infty} f(x) = h,
dann nennt man die Gerade yy = hh eine waagerechte (oder horizontale) Asymptote von ff. Analoges gilt für den Grenzwert x→−∞x \to -\infty.
Ist p: R→Rp:\, \R \to \R eine Funktion, der sich ff beim Grenzübergang nach +∞+\infty oder −∞-\infty beliebig annähert, d. h. gilt
lim⁡x→∞[f(x)−p(x)]=0\lim_{x\to\infty} [f(x)-p(x)] = 0 oder lim⁡x→−∞[f(x)−p(x)]=0,\lim_{x\to-\infty} [f(x)-p(x)] = 0,
dann nennt man pp eine schräge Asymptote von ff.
Durch Anwendung der Exponentialfunktion kommt man wieder zur asymptotischen Äquivalenz, wie oben formuliert.
Ist f=g/h f = g / h eine rationale Funktion (mit Polynomen gg und hh), dann hat ff stets eine schräge Asymptote nämlich das bei Polynomdivision von gg durch hh entstehende Polynom pp. Der senkrechte Abstand von ff zu pp wird durch die echt gebrochenrationale Restfunktion angegeben, die dieselben senkrechten Asymptoten wie ff hat und zusätzlich die waagerechte Asymptote yy = 0.

Beispiele

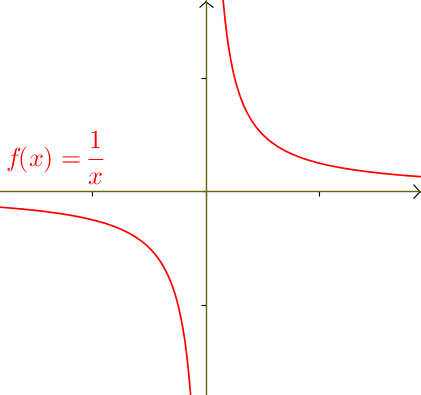
Asym2.png
Asymptoten von 1/x
Die Funktion (siehe Hyperbel)
f1(x)=1x f_1(x) = \dfrac{1}{x}
hat die Polstelle, bzw. senkrechte Asymptote bei xx = 0 und die waagerechte Asymptote yy = 00.
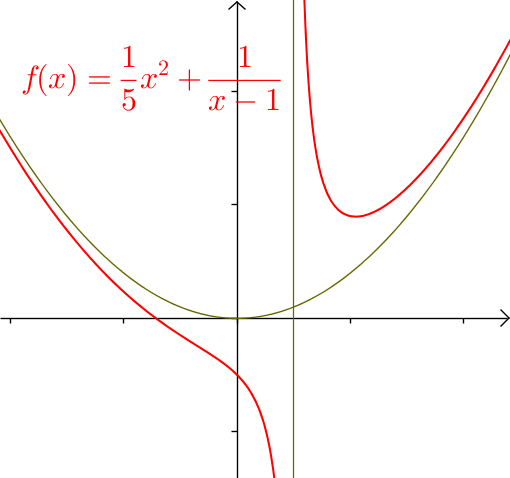
Asym3.png
Asymptoten von (x^3-x^2+5)/(5x-5)
Die Funktion
f2(x)=x3−x2+55x−5=x3−x25x−5+1x−1=15x2+1x−1 f_2(x) = \dfrac{x^3-x^2+5}{5x-5} = \dfrac{x^3-x^2}{5x-5}+ \dfrac{1}{x-1} = \dfrac{1}{5}x^2 + \dfrac{1}{x-1}
hat die Polstelle bei x=1 x = 1 und (wenn man Polynome als schräge Asymptoten zulässt) die Näherungsparabel p(x)=15x2p(x) = \dfrac{1}{5}x^2.

In der Mathematik gibt es keine Autoritäten. Das einzige Argument für die Wahrheit ist der Beweis.

K. Urbanik

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Asymptote aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen