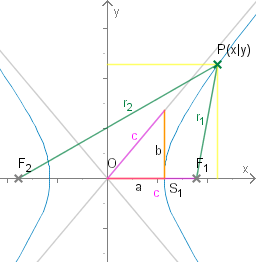
Die Hyperbel

Die Hyperbel ist die Menge aller Punkte der Ebene, wo die Differenz des Abstandes zu zwei vorgegebenen Punkten $F_1$ und $F_2$ den festen Wert $2a$ hat.

Sei $O$ der Mittelpunkt der Strecke $\overline{F_1F_2}$ und $c=\overline {OF_1}=\overline{F_2O}$. Für unsere Betrachtungen legen wir den Ursprung des Koordinatensystems in den Punkt $O$ und richten die $x$-Achse entlang der Strecke $\overline {OF_1}$ aus. Wenn die Hyperbel die $x$-Achse im Punkt $S_1$ schneidet, erkennt man, dass $a=\overline{OS_1}$ gilt.

Legen wir jetzt noch $b^2=c^2-a^2$ fest, können wir die folgende Formel für die Hyperbel angeben:

Es gilt nach dem Satz des Pythagoras:

Nach der Definition der Hyperbel gilt: und wenn wir (1) von (2) subtrahieren, ergibt sich: $r_2^2-r_1^2=4cx$. Also:

und

Zusammen mit (3) gilt dann: $r_2=a+ \dfrac c a x$. Setzen wir dieses Ergebnis in (2) ein, erhalten wir:

$\implies \braceNT{\dfrac {c^2}{a^2} -1}x^2-y^2=c^2-a^2$ $\implies \braceNT{\dfrac {c^2-a^2}{a^2} }x^2-y^2=c^2-a^2$ $\implies {\dfrac {b^2}{a^2} }x^2-y^2=b^2$ $\implies\dfrac {x^2}{a^2}-\dfrac {y^2}{b^2}=1$ $\qed$