Asymptoten der Hyperbel

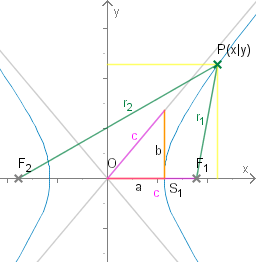
Die Hyperbel besitzt Geraden als Asymptoten. Um diese zu ermitteln setzen wir ihre Gleichung mit

y=mx

an. Dann ist

y^2=m^2x^2

.(1)

Stellen wir die Gleichung der Hyperbel (Formel 15VU) nach

y^2

um, ergibt sich:

y^2=\dfrac{b^2}{a^2}x^2-b^2

Damit eine Gerade der Form (1) Asymptote ist, muss

\lim_{x\rightarrow\infty}\dfrac {\dfrac{b^2}{a^2}x^2-b^2}{m^2x^2}=1

gelten. Da

\lim_{x\rightarrow\infty}\dfrac {b^2}{m^2x^2}=0

ist, kann dies aber nur für

m^2=\dfrac{b^2}{a^2}

der Fall sein und damit ist die Gleichung der Asymtoten:

y=\pm \dfrac b a x

Damit erklärt sich auch der in der Grafik gezeigte Zusammenhang von

a

b

und

c

Jede mathematische Formel in einem Buch halbiert die Verkaufszahl dieses Buches.

Stephen Hawking

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.

Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld • Dοrfplatz 25 • 17237 Blankеnsее • Tel.: 01734332309 (Vodafone/D2) • Email: cο@maτhepedιa.dе