Die Ellipse

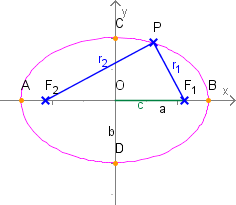
Ellipse.png
Die Ellipse ist die Menge aller Punkte der Ebene, die zu zwei vorgegebenen Punkten (den Brennpunkten) F1F_1 und F2F_2 einen festen Abstand 2a2a haben.
Für einen beliebigen Punkt PP der Ellipse gilt: 2a=r1+r22a=r_1+r_2.
Die Stecke AB‾=2a\overline{AB}=2a heißt große Achse der Ellipse, bei a=AO‾=OB‾a=\overline{AO}=\overline{OB} spricht man von der großen Halbachse. Analog heißt CD‾=2b\overline{CD}=2b die kleine Achse und b=CO‾=OD‾b=\overline{CO}=\overline{OD} sind demnach die kleinen Halbachsen.
Die Ellipsengleichung muss auch im Punkt CC erfüllt sein muss. Dann gilt aber a=r1=r2a=r_1=r_2 und mit c=OF1‾=F2O‾c=\overline{OF_1}=\overline{F_2O} sowie unter Benutzung des Satzes des Pythagoras erhält man die Formel:
c2+b2=a2c^2+b^2=a^2.(1)
Die Länge cc kann man also aus
c=a2−b2c=\sqrt{a^2-b^2}
bestimmen.
Für die Gleichungen der Ellipse spricht man von der Normalform, wenn der Mittelpunkt der Ellipse mit dem Koordinatenursprung und die Halbachsen mit den Koordinatenachsen zusammenfallen.

Formel 15VN (Gleichung der Ellipse in Normalform)

x2a2+y2b2=1\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1,
mit den Halbachsen aa und bb.
Für einen Kreis (r=a=br=a=b) geht die Formel in Formel 15VR über.

Herleitung

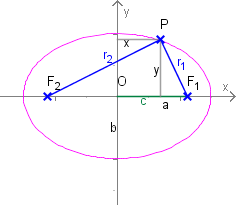
EllipseGl.png
Für einen Punkt P(x∣y)P(x|y) auf der Ellipse gilt:
r12=(x−c)2+y2r_1^2=(x-c)^2+y^2 =x2+c2−2cx+y2=x^2+c^2-2cx+y^2,(2)
r22=(x+c)2+y2r_2^2=(x+c)^2+y^2 =x2+c2+2cx+y2=x^2+c^2+2cx+y^2.(3)
Nach der Subtraktion der Gleichungen (2) von Gleichung (3):
r22−r12=4cxr_2^2-r_1^2=4cx.
Dann gilt auch:
4cx=r22−r12=(r2+r1)(r2−r1)=2a(r2−r1)4cx=r_2^2-r_1^2=(r_2+r_1)(r_2-r_1)=2a(r_2-r_1),
also r2−r1=2⋅cxar_2-r_1=2\cdot\dfrac{cx} a. Zusammen mit r2+r1=2ar_2+r_1=2a ergibt sich:
r2=a+cxar_2=a+\dfrac{cx} a(4)
und
r1=a−cxar_1=a-\dfrac{cx} a
Letzteres brauchen wir für die Herleitung von Formel 15VO.
Setzen wir nun (4) in (3) ein, erhalten wir:
(a+cxa)2=a2+(ca)2x2+2cx=x2+c2+2cx+y2{\braceNT{a+\dfrac{cx} a}}^2=a^2+{\braceNT{\dfrac c a}}^2x^2+2cx=x^2+c^2+2cx+y^2
Benutzen wir nun (1):
a2+(1−b2a2)x2=x2+y2+a2−b2a^2+{\braceNT{1-\dfrac {b^2} {a^2}}}x^2=x^2+y^2 +a^2-b^2,
woraus folgt:
b2=b2a2x2+y2b^2=\dfrac {b^2} {a^2}x^2+y^2,
und nach der Division durch b2b^2 ergibt sich die Behauptung. □\qed
 
 

Miß alles, was sich messen läßt, und mach alles meßbar, was sich nicht messen läßt.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene