Gleichung der Ellipse in Polarkoordinaten

Zur Vorbereitung der Herleitung der Gleichung der Ellipse in Polarkoordinaten führen wird folgende Bezeichnungen ein: Die Exzentrizität ϵ\epsilon ist der Quotient aus Brennweite cc und großer Halbachse aa:
ϵ=ca\epsilon=\dfrac c a.
Die Exzentrizität ist damit immer kleiner als 1 und für ϵ=0\epsilon=0 degeneriert die Ellipse zum Kreis.
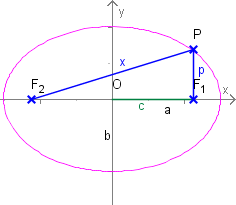
EllipseP.png
Als weitere Abkürzung führen wir p=b2ap=\dfrac {b^2} a ein. Diese Größe entspricht der halben Länge der Strecke, die durch einen Brennpunkt parallel zur kleinen Achse verläuft.
Es gilt nämlich einerseits p+x=2ap+x=2a (Definition der Ellipse) und andererseits p2+(2c)2=x2p^2+(2c)^2=x^2 (Satz des Pythagoras). Damit erhalten wir p2+4c2=(2a−p)2=4a2−4ap+p2p^2+4c^2=(2a-p)^2=4a^2-4ap+p^2; also 4c2=4a2−4ap4c^2=4a^2-4ap ⇒p=a2−c2a=b2a\Rightarrow p=\dfrac {a^2-c^2} a=\dfrac {b^2} a.
Mit den obigen Definitionen geben wir nun

Formel 15VO (Gleichung der Ellipse in Polarkoordinaten)

r=p1+ϵcos⁡φr=\dfrac p{1+\epsilon\cos\phi}    (für ϵ<1\epsilon<1)

Herleitung

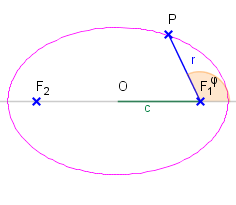
EllipsePolK.png
Wir legen den Ursprung in den Brennpunkt F1F_1 und messen den Winkel φ\phi mit der großen Halbachse.
Aus dem Beweis von Formel 15VN entnehmen wir
r=r1=a−cax=a−ca⋅(c+rcos⁡φ)r=r_1=a-\dfrac{c} a x=a-\dfrac c a \cdot(c+r\cos\phi) (Formel 15VQ und Verschiebung des Ursprungs)
⇒r=a−c2a−ϵrcos⁡φ\Rightarrow r=a-\dfrac {c^2} a-\epsilon r \cos\phi =a2−c2a−ϵrcos⁡φ=\dfrac {a^2-c^2} a-\epsilon r \cos\phi =b2a−ϵrcos⁡φ=p−ϵrcos⁡φ=\dfrac {b^2} a-\epsilon r \cos\phi=p-\epsilon r \cos\phi
⇒(1+ϵcos⁡φ)⋅r=p\Rightarrow (1+\epsilon\cos\phi)\cdot r =p, woraus die Behauptung sofort ersichtlich ist. □\qed
 
 

Das Buch der Natur ist mit mathematischen Symbolen geschrieben.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Kurven 2. Ordnung