Ebene Polarkoordinaten

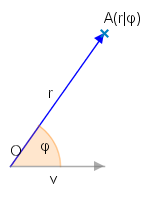
PKoord.png
Neben den kartesischen Koordinaten, die auf einem geradlinigen Koordinatensystem beruhen, sind auch krummlinige Koordinaten möglich. Von besonderer Bedeutung sind die Polarkoordinaten. Sie sind durch einen Ursprungspunkt OO, den Pol, und eine ausgezeichnete Richtung vv charakterisiert. Punkte in der Ebene werden über zwei Koordinaten, den Winkel φ\phi mit dem Richtungsvektor vv und dem Abstand rr des Punktes vom Pol gekennzeichnet.
Alle Punkte der Ebene (bis auf den Pol) sind im Polarkoordinatensystem eindeutig darstellbar. Für den Pol gilt bei r=0r=0, dass der Winkel φ\phi beliebig gewählt sein kann.
 
 

Beziehungen zu kartesischen Koordinaten

Für die Umrechung von kartesischen und Polarkoordinaten nehmen wir an, dass die Ursprünge zusammenfallen und die Richtung der Polarkoordinaten in Richtung der xx-Achse verläuft.
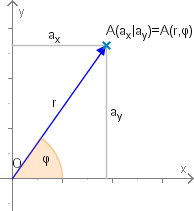
PKoordUr.png
Sei der Punkt AA mit den kartesischen Koordinaten A(ax∣ay)A(a_x|a_y) und den Polarkoordinaten A(r∣φ)A(r|\phi) gegeben, dann gelten folgenden Beziehungen:

Formel 15VP (Umrechnung von kartesischen in Polarkoordinaten)

r2=ax2+ay2r^2=a_x^2+a_y^2
tan⁡φ=ayax\tan\phi=\dfrac {a_y}{a_x}
Diese leiten sich aus dem Satz des Pythagoras bzw. der Definition des Tangens her.
Hieraus kann man bei gegebenen kartesischen Koordinaten die Polarkoordinaten bestimmen.
Andererseits gilt mit den Definitionen von Sinus und Cosinus:

Formel 15VQ (Umrechnung von Polarkoordinaten in kartesische Koordianten)

ax=r⋅cos⁡φa_x=r\cdot \cos\phi
ay=r⋅sin⁡φa_y=r\cdot \sin\phi,
womit man aus gegebenen Polarkoordinaten die kartesischen Koordinaten bestimmen kann.

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene