Koordinatentransformationen in der Ebene

Wir gehen bei der Transformation von üblichen rechtwinkligen Koordinatensystem aus.

Verschiebung

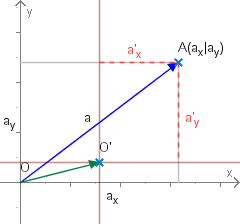
KoVer.png
Der Ursprung O′O' des Koordinatensystems (O′,x′,y′)(O',x',y') habe im Koordinatensystem (O,x,y)(O,x,y) die Koordinaten (ox,oy)(o_x,o_y). Die Achsen seien parallel.
Ein beliebiger Punkt AA mit den Koordinaten A(ax∣ay)A(a_x|a_y) im OO- Koordinatensystem hat dann im O′O' Koordinatensystem die Koordinaten
A(ax′,ay′)=(ax−ox,ay−oy)A(a'_x,a'_y)=(a_x-o_x,a_y-o_y)
.
Diese Gleichung beschreibt den Übergang vom OO ins O′O' System. In Vektorschreibweise: a′=a−oa'=a-o.
 
 

Drehung

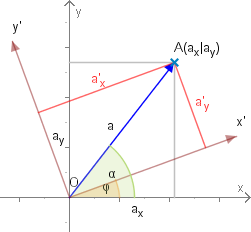
KoDrehr.png
Seien nun die beiden Ursprünge identisch und die Achsen um den Winkel φ\phi gegen den Uhrzeigersinn gedreht.
Ein Punkt AA habe im x,yx,y-System die Koordinaten A(ax∣ay)A(a_x|a_y) und der Winkel mit der xx-Achse ist α\alpha. Dann gilt für die Koordinaten im x′,y′x',y'-System:
ax′=∣∣a∣∣⋅cos⁡(α−φ)a'_x=||a||\cdot\cos(\alpha-\phi)
ay′=∣∣a∣∣⋅sin⁡(α−φ)a'_y=||a||\cdot\sin(\alpha-\phi)
Nach Satz 5220A gilt dann:
ax′=∣∣a∣∣⋅(cos⁡α⋅cos⁡φ+sin⁡α⋅sin⁡φ)a'_x=||a||\cdot(\cos\alpha \cdot\cos\phi+ \sin\alpha \cdot\sin\phi) ay′=∣∣a∣∣⋅(sin⁡α⋅cos⁡φ−cos⁡α⋅sin⁡φ)a'_y=||a||\cdot(\sin\alpha\cdot\cos\phi - \cos\alpha\cdot\sin\phi).(1)
Im x,yx,y-System ist:
sin⁡α=ay∣∣a∣∣\sin\alpha=\dfrac {a_y}{||a||} cos⁡α=ax∣∣a∣∣\cos\alpha=\dfrac {a_x}{||a||}.
Setzen wir dies in (1) ein, so erhalten wir:
ax′=ax⋅cos⁡φ+ay⋅sin⁡φa'_x=a_x \cdot\cos\phi+ a_y \cdot\sin\phi
ay′=−ax⋅sin⁡φ+ay⋅cos⁡φa'_y=-a_x \cdot\sin\phi+ a_y \cdot\cos\phi.
In Vektorschreibweise:
(ax′ay′)=(cos⁡φsin⁡φ−sin⁡φcos⁡φ)(axay)\pmatrix{{a'_x}\\ {a'_y}}=\pmatrix{{\cos\phi}&{\sin\phi} \\ {-\sin\phi}&{\cos\phi}} \pmatrix{{a_x}\\ {a_y}} .(2)
Die in (2) auftretende Matrix heißt Drehmatrix.

Religion und Mathematik sind nur verschiedene Ausdrucksformen derselben göttlichen Exaktheit.

Kardinal Michael Faulhaber

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene