Polynome

Ein Polynom ist eine reelle Funktion der Form
f(x)=∑i=0naixi=a0+a1x+a2x2+…+anxnf(x)=\sum\limits_{i=0}^n {a_ix^i}=a_0+a_1x+a_2x^2+\ldots+a_nx^n
dabei sei n∈Nn\in \dom N und an∈Ra_n\in \dom R, an≠0a_n\neq0. Polynome heißen auch ganzrationale Funktionen.
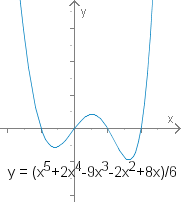
Polynom.png
Die Zahl nn heißt Grad des Polynoms und wird mit deg⁡(f)\deg(f) bezeichnet. Die aia_i sind die Koeffizienten des Polynoms, wobei ana_n der Leitkoeffizient ist.
Für den Grad von Polynomen ff und gg gilt:
deg⁡(f+g)≤max⁡(deg⁡f,deg⁡g) \deg(f+g) \le \max(\deg f, \deg g)
deg⁡(f⋅g)=deg⁡f+deg⁡g  \deg(f\cdot g) = \deg f + \deg g\,
 
 

Spezielle Polynome

Konstante Funktion

y=f(x)=cy=f(x)=c für ein festes c∈Rc\in\dom R ist die konstante Funktion.
Als Polynom betrachtet hat die konstante Funktion den Grad 0.

Identische Funktion

y=f(x)=xy=f(x)=x
Die identische Funktion ist eine spezielle lineare Funktion. Als Polynom betrachtet hat sie den Grad 1.
Polynome des Grades
  • 1 heißen lineare Funktionen (z. B. fP(x)=1x+3fP(x) = 1x + 3 ).
  • 2 heißen quadratische Funktionen (z. B. P(x)=−3x2−x+3 P(x) = -3x^2-x + 3 ).
  • 3 heißen kubische Funktionen (z. B. P(x)=6x3−3x2+5x+1 P(x) = 6x^3-3x^2+5x + 1 ).
  • 4 heißen quartische Funktionen (z. B. P(x)=−3x3−x2+3x+1 P(x) = -3x^3-x^2+3x + 1 ).

Nullstellen

Ist x0x_0 eine Nullstelle von f(x)=∑i=0naixi=a0+a1x+…+anxnf(x)=\sum\limits_{i=0}^n {a_ix^i}=a_0+a_1x+\ldots+a_nx^n, so gibt es ein Polynom f1f_1vom Grad n−1n-1, sodass f(x)=(x−x0)⋅f1(x)f(x)=(x-x_0)\cdot f_1(x).
Allgemein gilt: sind x0x_0, x1x_1, ... xlx_l Nullstellen von ff, so gibt es ein Polynom gg von Grad n−ln-l, sodass f(x)=(x−x0)⋅(x−x1)⋅⋯⋅(x−xl)⋅g(x)f(x)=(x-x_0)\cdot (x-x_1)\cdot \dots\cdot (x-x_l)\cdot g(x). Dies folgt aus dem Fundamentalsatz der Algebra.

Definition

Eine reelle Zahl x0x_0 heißt kk-fache Nullstelle (oder Nullstelle kk-ter Ordnung) von ff, wenn es ein Polynom fkf_k vom Grad n−kn-k gibt, sodass f(x)=(x−x0)k⋅fk(x)f(x)=(x-x_0)^k\cdot f_k(x) und fk(x0)≠0f_k(x_0)\neq 0.
Ein Polynom vom Grad nn kann also maximal nn verschiedene Nullstellen besitzen. Besitzt es genau nn (nicht notwendigerweise verschiedene) Nullstellen, kann man es als Produkt von nn Linearfaktoren darstellen:
f(x)=∏i=1n(x−xi)f(x)=\prod\limits_{i=1}^n(x-x_i),
wobei die xix_i (i=1…n)i=1\dots n) die Nullstellen von ff sind.

Beispiele

  1. f(x)=x4−2x3−x+2f(x)=x^4-2x^3-x+2 hat die nur beiden Nullstellen x1=1x_1=1 und x2=2x_2=2, es gilt f(x)=x4−2x3−x+2f(x)=x^4-2x^3-x+2 =(x2+x+1)⋅(x−1)⋅(x−2)=(x^2+x+1)\cdot(x-1)\cdot(x-2).
  2. f(x)=x7−6x6+13x5−13x4+10x3−13x2+12x−4f(x)= x ^{7} - 6 x ^{6} + 13 x ^{5} - 13 x ^{4} + 10 x ^{3} - 13 x ^{2} + 12 x - 4 hat die dreifache Nullstelle x1=1x_1=1 und die doppelte Nullstelle x2=2x_2=2; es gilt f(x)=(x2+x+1)⋅(x−1)3⋅(x−2)2f(x)=( x ^{2} + x + 1) \cdot( x - 1) ^{3} \cdot( x - 2) ^{2}.

Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.

Jakob I. Bernoulli

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen